题目内容
 如图,正方形DEFG的边EF在△ABC的边BC上,D,G分别在边AB,AC上,AH⊥BC,BC=10,AH=6,则正方形边长为________.
如图,正方形DEFG的边EF在△ABC的边BC上,D,G分别在边AB,AC上,AH⊥BC,BC=10,AH=6,则正方形边长为________.
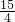
分析:由DG∥BC得△ADG∽△ABC,利用相似三角形对应边上高的比等于相似比,列方程求解.
解答:设正方形的边长为x.
由正方形DEFG得,DG∥EF,即DG∥BC,
∵AH⊥BC,
∴AP⊥DG.
由DG∥BC得△ADG∽△ABC
∴
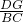 =
=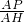 .
.∵PH⊥BC,DE⊥BC
∴PH=ED,AP=AH-PH,
即
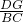 =
= ,
,由BC=10,AH=6,DE=DG=x,
得
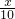 =
=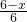 ,
,解得x=
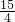 .
.故正方形DEFG的边长是
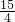 .
.故答案为:
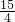 .
.点评:本题考查了相似三角形的判定与性质.关键是由平行线得到相似三角形,利用相似三角形的性质列方程.

练习册系列答案
相关题目
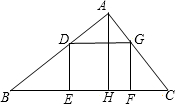 如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8,求正方形DEFG的边长.
如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8,求正方形DEFG的边长.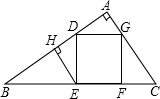 已知:如图,正方形DEFG内接入Rt△ABC,EF在斜边BC上,EH⊥AB于H.
已知:如图,正方形DEFG内接入Rt△ABC,EF在斜边BC上,EH⊥AB于H. 如图,正方形DEFG的边EF在△ABC的边BC上,D,G分别在边AB,AC上,AH⊥BC,BC=10,AH=6,则正方形边长为
如图,正方形DEFG的边EF在△ABC的边BC上,D,G分别在边AB,AC上,AH⊥BC,BC=10,AH=6,则正方形边长为 如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8,求正方形DEFG的边长.
如图,正方形DEFG的边EF在△ABC的边BC上,顶点D、G分别在边AB、AC上,AH⊥BC,垂足为H.已知BC=12,AH=8,求正方形DEFG的边长.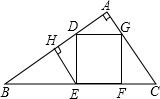 已知:如图,正方形DEFG内接入Rt△ABC,EF在斜边BC上,EH⊥AB于H.
已知:如图,正方形DEFG内接入Rt△ABC,EF在斜边BC上,EH⊥AB于H.