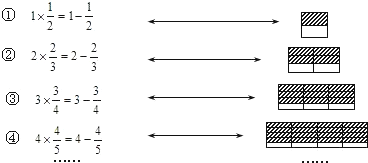
题目内容
【题目】我区在修筑渭河堤防工程时,欲拆除河岸边的一根电线杆AB.如图,已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡度为1:0.5,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间的宽是2米,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将DE段封止?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域)
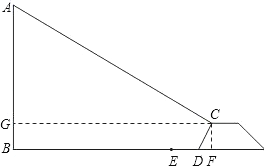
【答案】没有必要封止DE.
【解析】
试题分析:根据题意分析图形可得:在Rt△CDF中,由CF=2,tan∠CDF=2,可求得DE,进而得到BE的长.解Rt△AGC可得BE的值,通过比较BE、AB的大小即可求出答案.
解:∵i=1:0.5,CF=2米
∴tan∠CDF=![]() =2,
=2,
∴DF=1米,BG=2米,
∵BD=14米,
∴BF=GC=15米.
在Rt△AGC中,AG=15tan30°=15×![]() =5
=5![]() ≈8.66(米),
≈8.66(米),
∴AB=AG+BG=8.66+2=10.66米,BE=BD﹣DE=14﹣2=12(米),
∵10.66<12,
∴没有必要封止DE.

练习册系列答案
相关题目