Question

（2013•大兴区二模）如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的动点，则线段OM长的最小值为

3

．

Answer 1

分析：过O作OM⊥AB于M，此时线段OM的长最短，连接OA，根据垂径定理求出AM，根据勾股定理求出OM即可．

解答：解：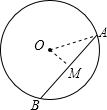
过O作OM⊥AB于M，此时线段OM的长最短，连接OA，
∵OM过O，OM⊥AB，
∴AM=

1

2

AB=

1

2

×8=4，
在Rt△AMO中，由勾股定理得：OM=

OA2-AM2

=

52-42

=3，
故答案为：3．

点评：本题考查了垂径定理，勾股定理，垂线段最短的应用，关键是确定M的位置和求出OM长．