题目内容
如图,一次函数的图象与x轴、y轴分别交于A、B两点,且A点的坐标为(| 2 |
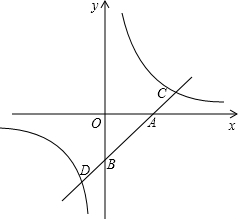 D分别在第一、三象限,且此一次函数与反比例函数图象交于C、D两点,又OA=OB=AC=BD.
D分别在第一、三象限,且此一次函数与反比例函数图象交于C、D两点,又OA=OB=AC=BD.(1)求一次函数与反比例函数的解析式.
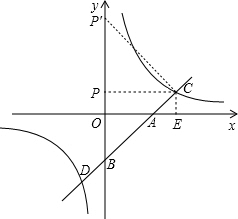
(2)在y轴上是否存在点P,使△BCP为等腰直角三角形?若存在,请写出所有符合条件的P点坐标(不用写出计算过程);若不存在,请说明理由.
分析:(1)作CE⊥x轴于E,由OA=OB可知△ACE是等腰直角三角形,OA=OB,且A(
,0),则B(0,-
)代入一次函数的解析式为y=kx+b可求直线AB的解析式,由AC=
,可求AE=CE=1,故C(1+
,1),代入反比例函数的解析式为y=
可求反比例函数的解析式;
(2)过C点作CP⊥y轴,或过c点作CP⊥AC,交y轴于P′,根据等腰直角三角形的性质可求满足条件的P点坐标.
| 2 |
| 2 |
| 2 |
| 2 |
| m |
| x |
(2)过C点作CP⊥y轴,或过c点作CP⊥AC,交y轴于P′,根据等腰直角三角形的性质可求满足条件的P点坐标.
解答:解:(1)设一次函数的解析式为y=kx+b(k≠0),反比例函数的解析式为y=
(m≠O),
∵OA=OB,A(
,0),
∴B(0,-
),
∴可得:
,解得:
,
∴y=x-
,
作CE⊥x轴于E,则△ACE是等腰直角三角形,
∴AE=CE=
sin45°=1,
∴C(1+
,1),
∴1=
,解得m=1+
,
∴y=
;
(2)存在,P点坐标分别是(0,1)或(0,2+
).
| m |
| x |
∵OA=OB,A(
| 2 |
∴B(0,-
| 2 |
∴可得:
|
|

∴y=x-
| 2 |
作CE⊥x轴于E,则△ACE是等腰直角三角形,
∴AE=CE=
| 2 |
∴C(1+
| 2 |
∴1=
| m | ||
1+
|
| 2 |
∴y=
1+
| ||
| x |
(2)存在,P点坐标分别是(0,1)或(0,2+
| 2 |
点评:本题考查了点的坐标的求解与一次函数、反比例函数关系式的确定方法.运用待定系数法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知反比例函数y=
如图,已知反比例函数y=
 解答:
解答:
