题目内容
(1)探索:解下列方程,将得到的两根x1,x2和x1+x2,x1•x2的值填入下面的表格.| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2+3x-4=0 | ||||
| 2x2+x-1=0 | ||||
| 3x2-5x+2=0 |
(3)利用一元二次方程的求根公式证明(2)中的猜想.
【答案】分析:(1)对方程分解因式求解:
第一个:(x+4)(x-1)=0,x1=-4,x2=1;
第二个:(2x-1)(x+1)=0,x1= ,x2=-1;
,x2=-1;
第三个:(3x-2)(x-1)=0,x1= ,x2=1.并分别计算出两根之积,两根之和填入表格中.
,x2=1.并分别计算出两根之积,两根之和填入表格中.
(2)(3)首先求出方程的两个实根,求和,求积,即可证明根与系数的关系为:x1+x2=- ,x1x2=
,x1x2= .
.
解答:解:(1)
(2)根与系数的关系为:x1+x2=- ,x1x2=
,x1x2= .
.
(3)对于方程:ax2+bx+c=0(a≠0,且a,b,c是常数),当△≥0时,利用求根公式,得
x1=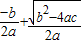 ,x2=
,x2= -
- .
.
x1+x2= +
+ -
- =-
=- ,
,
x1x2=( )•(
)•(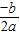 -
- )=(
)=( )2-(
)2-(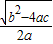 )2=
)2= .
.
∴x1+x2=- ,x1x2=
,x1x2=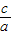 是正确的.
是正确的.
点评:本题是找规律题,首先通过计算求出各个方程的根,观察后得出猜测,再用求根公式进行证明.
第一个:(x+4)(x-1)=0,x1=-4,x2=1;
第二个:(2x-1)(x+1)=0,x1=
 ,x2=-1;
,x2=-1;第三个:(3x-2)(x-1)=0,x1=
 ,x2=1.并分别计算出两根之积,两根之和填入表格中.
,x2=1.并分别计算出两根之积,两根之和填入表格中.(2)(3)首先求出方程的两个实根,求和,求积,即可证明根与系数的关系为:x1+x2=-
 ,x1x2=
,x1x2= .
.解答:解:(1)
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2+3x-4=0 | -4 | 1 | -3 | -4 |
| 2x2+x-1=0 |  | -1 | - | - |
| 3x2-5x+2=0 |  | 1 |  |  |
 ,x1x2=
,x1x2= .
.(3)对于方程:ax2+bx+c=0(a≠0,且a,b,c是常数),当△≥0时,利用求根公式,得
x1=
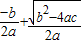 ,x2=
,x2= -
- .
.x1+x2=
 +
+ -
- =-
=- ,
,x1x2=(
 )•(
)•(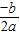 -
- )=(
)=( )2-(
)2-(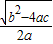 )2=
)2= .
.∴x1+x2=-
 ,x1x2=
,x1x2=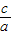 是正确的.
是正确的.点评:本题是找规律题,首先通过计算求出各个方程的根,观察后得出猜测,再用求根公式进行证明.

练习册系列答案
相关题目
(1)探索:解下列方程,将得到的两根x1,x2和x1+x2,x1•x2的值填入下面的表格.
(2)猜想:x1+x2,x1•x2的值与一元二次方程ax2+bx+c=0(a≠0)(x1,x2是其两个根)的各项系数a,b,c之间有何关系?
(3)利用一元二次方程的求根公式证明(2)中的猜想.
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2+3x-4=0 | ||||
| 2x2+x-1=0 | ||||
| 3x2-5x+2=0 |
(3)利用一元二次方程的求根公式证明(2)中的猜想.
(1)探索:解下列方程,将得到的两根x1,x2和x1+x2,x1•x2的值填入下面的表格.
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2+3x-4=0 | ||||
| 2x2+x-1=0 | ||||
| 3x2-5x+2=0 |
(3)利用一元二次方程的求根公式证明(2)中的猜想.
(1)探索:解下列方程,将得到的两根x1,x2和x1+x2,x1•x2的值填入下面的表格.
(2)猜想:x1+x2,x1•x2的值与一元二次方程ax2+bx+c=0(a≠0)(x1,x2是其两个根)的各项系数a,b,c之间有何关系?
(3)利用一元二次方程的求根公式证明(2)中的猜想.
| 方程 | x1 | x2 | x1+x2 | x1•x2 |
| x2+3x-4=0 | ||||
| 2x2+x-1=0 | ||||
| 3x2-5x+2=0 |
(3)利用一元二次方程的求根公式证明(2)中的猜想.