题目内容
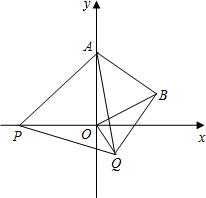
 平面直角坐标系中,已知点O(0,0)、A(0,2)、B(1,0),点P是反比例函数y=-
平面直角坐标系中,已知点O(0,0)、A(0,2)、B(1,0),点P是反比例函数y=-| 1 |
| x |
(
,-
)或(-
,
)或(
,-
)或(-
,
)
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
(
,-
)或(-
,
)或(
,-
)或(-
,
)
.| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
分析:由A(0,2)、B(1,0),可求得OA与OB的长,然后分别从当
=
,即OQ=2PQ时,△OPQ∽△ABO与当
=
,即PQ=2OQ时,△OPQ∽△BAO去分析求解即可求得答案.
| PQ |
| BO |
| OQ |
| OA |
| PQ |
| AO |
| OQ |
| OB |
解答:解:∵A(0,2)、B(1,0),
∴OA=2,OB=1,
∵PQ⊥x轴,
∴∠PQO=∠AOB=90°,
当
=
,即OQ=2PQ时,△OPQ∽△ABO,
设点P(x,-
x),
∴-
x=-
,
解得:x=±
,
∴点P的坐标是:(
,-
)或(-
,
);
当
=
,即PQ=2OQ时,△OPQ∽△BAO,
设点P(x,-2x),
∴-2x=-
,
解得:x=±
,
∴点P的坐标是:(
,-
)或(-
,
).
综上可得:点P的坐标是:(
,-
)或(-
,
)或(
,-
)或(-
,
).
故答案为:(
,-
)或(-
,
)或(
,-
)或(-
,
).
∴OA=2,OB=1,
∵PQ⊥x轴,
∴∠PQO=∠AOB=90°,
当
| PQ |
| BO |
| OQ |
| OA |
设点P(x,-
| 1 |
| 2 |
∴-
| 1 |
| 2 |
| 1 |
| x |
解得:x=±
| 2 |
∴点P的坐标是:(
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
当
| PQ |
| AO |
| OQ |
| OB |
设点P(x,-2x),
∴-2x=-
| 1 |
| x |
解得:x=±
| ||
| 2 |
∴点P的坐标是:(
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
综上可得:点P的坐标是:(
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
故答案为:(
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| 2 |
点评:此题考查了相似三角形的判定与性质以及反比例函数上点的性质.此题难度适中,注意掌握方程思想、分类讨论思想与数形结合思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B.
一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B. 21、如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
21、如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.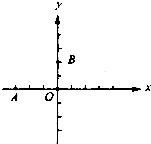 18、如图,在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是O(0,0),A(-3,0),B(0,2),求平行四边形第四个顶点C的坐标.
18、如图,在平面直角坐标系中,已知平行四边形的三个顶点坐标分别是O(0,0),A(-3,0),B(0,2),求平行四边形第四个顶点C的坐标.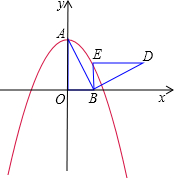 出M在抛物线内部(指抛物线与X轴所围成的部分)时t的取值范围.
出M在抛物线内部(指抛物线与X轴所围成的部分)时t的取值范围.