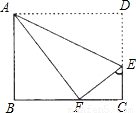
题目内容
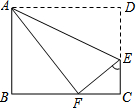 为了向建国六十周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:
为了向建国六十周年献礼,某校各班都在开展丰富多彩的庆祝活动,八年级(1)班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:①先裁下了一张长BC=20cm,宽AB=16cm的矩形纸片ABCD,
②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,
请你根据①②步骤解答下列问题:计算EC,FC的长.
分析:由轴对称的性质可以得出△ADE≌△AFE,就可以得出EF=ED,设CE=x,由勾股定理就可以求出结论.
解答:解:∵△ADE由△AFE关于AE对称,
∴△ADE≌△AFE,
∴DE=FE.AD=AF,
∵BC=20cm,AB=16cm,
∴CD=16cm,AD=AF=20cm,
在Rt△ABF中,由勾股定理,得
BF=12cm.
∴CF=20-12=8cm.
∵四边形ABCD是矩形,
∴∠C=90°.
设CE=x,则DE=EF=16-x,在Rt△CEF中,由勾股定理,得
(16-x)2=64+x2,
解得:x=6.
∴EC=6.
答:EC=6cm,CF=8cm.
∴△ADE≌△AFE,
∴DE=FE.AD=AF,
∵BC=20cm,AB=16cm,
∴CD=16cm,AD=AF=20cm,
在Rt△ABF中,由勾股定理,得
BF=12cm.
∴CF=20-12=8cm.
∵四边形ABCD是矩形,
∴∠C=90°.
设CE=x,则DE=EF=16-x,在Rt△CEF中,由勾股定理,得
(16-x)2=64+x2,
解得:x=6.
∴EC=6.
答:EC=6cm,CF=8cm.
点评:本题考查了轴对称的性质的运用,勾股定理的运用,解答时运用轴对称的性质求解是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
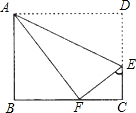 =16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,…请你根据①②步骤解答下列问题:
=16cm的矩形纸片ABCD,②将纸片沿着直线AE折叠,点D恰好落在BC边上的F处,…请你根据①②步骤解答下列问题: