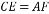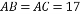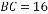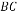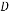题目内容
如图,Rt△ABC中,CD是斜边AB上的高,角平分线AE交CD于H,EF⊥AB于F,则下列结论中不正确的是( )

A.CH=HD B.∠ACD=∠B C.CH=CE=EF D.AC=AF
A.
【解析】
试题分析:根据角的平分线的性质,得CE=EF,两直线平行,内错角相等,得∠AEF=∠CHE,用AAS判定△ACE≌△AEF,由全等三角形的性质,得∠CEH=∠AEF,用等角对等边判定边相等.
A、点H不是CD的中点,故错误.
B、∵∠B和∠ACD都是∠CAB的余角,
∴∠ACD=∠B,故正确;
C、∵CD⊥AB,EF⊥AB,∴EF∥CD
∴∠AEF=∠CHE,
∴∠CEH=∠CHE
∴CH=CE=EF,故正确;
D、∵角平分线AE交CD于H,
∴∠CAE=∠BAE,
又∵∠ACB=∠AFE=90°,AE=AE,
∴△ACE≌△AEF,
∴CE=EF,∠CEA=∠AEF,AC=AF,故正确;
故选A.
考点: 1.角平分线的性质;2.全等三角形的判定与性质.

练习册系列答案
相关题目
某中学为了了解全校的耗电情况,抽查了10天中全校每天的耗电量,数据如下表:
千瓦时 | 90 | 93 | 102 | 113 | 114 | 120 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)写出上表中数据的众数和平均数.
(2)根据上题获得的数据,估计该校一个月的耗电量(按30天计算).
(3)若当地每千瓦时电的价格是0.5元,写出该校应付电费y(元)与天数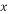 (
(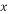 取正整数,单位:天)的函数关系式.
取正整数,单位:天)的函数关系式.