题目内容
【题目】已知△ABC为等边三角形,D为AC的中点,∠EDF=120°,DE交线段AB于E,DF交直线BC于F.
(1)如图(1),求证:DE=DF;
(2)如图(2),若BE=3AE,求证:CF=![]() BC.
BC.
(3)如图(3),若BE=![]() AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.
AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.

【答案】(1)证明见解析;(2)证明见解析;(3)![]() ,
,![]() .
.
【解析】
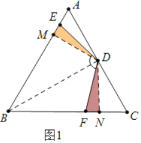
(1)如图1中,连接BD,作DM⊥AB于M,DN⊥BC于N,证明△DME≌△DNF即可得到结论;
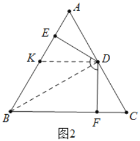
(2)如图2中,作DK∥BC交AB于K.设AE=a,则BE=3a,AB=AC=BC=4a,证明∠DFB=90°,求出CF即可解决问题;
(3)①如图3中,作DK∥BC交AB于K.只要证明△EDK≌△FDC,即可解决问题;
②如图4中,由(1)可知EM=FN,设AE=a,则BE=4a,AB=BC=AC=5a,AM=CN=![]() ,EM=FN=
,EM=FN=![]() a,可得CF=FN+CN=
a,可得CF=FN+CN=![]() a,由此即可 解决问题;
a,由此即可 解决问题;
证明:(1)如图1中,连接BD,作DM⊥AB于M,DN⊥BC于N,
∵∠DMB=∠DNB=90°,∠ABC=60°,
∴∠MDN=∠EDF=120°,
∴∠MDE=∠NDF,
∵△ABC是等边三角形,AD=DC,
∴∠DBA=∠DBC,
∴DM=DN,
∴△DME≌△DNF,
∴DE=DF.
(2)如图2中,作DK∥BC交AB于K.设AE=a,则BE=3a,AB=AC=BC=4a,
∵AD=DC,DK∥CB,
∴AK=BK=2a,DK=![]() BC=2a=AD=AK,
BC=2a=AD=AK,
∴AE=EK=a,
∴DE⊥AK,
∴∠BED=90°,
∵∠BED+∠BFD=180°,
∴∠DFB=90°,
在Rt△CDF中,∵∠C=60°,
∴CF=![]() CD=a,
CD=a,
∴CF=![]() BC.
BC.
(3)①如图3中,作DK∥BC交AB于K.
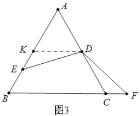
设BE=a,则AE=3a,AK=BK=2a,△ADK是等边三角形,
∴∠ADK=60°,∠EDF=∠KDC,
∴∠KDE=∠CDE,
∵DK=DC,DE=DF,
∴△EDK≌△FDC,
∴EK=CF=a,
∵BC=4a,
∴CF=![]() BC.
BC.
②如图4中,由(1)可知EM=FN,
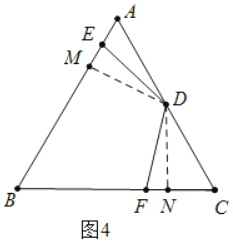
设AE=a,则BE=4a,AB=BC=AC=5a,AM=CN=![]() ,EM=FN=
,EM=FN=![]() a,
a,
∴CF=FN+CN=![]() a,
a,
∴CF:BC=![]() a:5a=3:10,
a:5a=3:10,
∴CF=![]() BC.
BC.
故答案为![]() ,
,![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解九(1)班学生的体温情况,对这个班所有学生测量了一次体温(单位:℃),小明将测量结果绘制成如下统计表和如图所示的扇形统计图.下列说法错误的是( )
体温(℃) | 36.1 | 36.2 | 36.3 | 36.4 | 36.5 | 36.6 |
人数(人) | 4 | 8 | 8 | 10 | x | 2 |
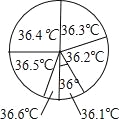
A.这些体温的众数是8
B.这些体温的中位数是36.35
C.这个班有40名学生
D.x=8