Question

【题目】如图，点P是矩形ABCD的边AD上的一动点，矩形的两条边AB、BC的长分别是6和8，则点P到矩形的两条对角线AC和BD的距离之和是 ．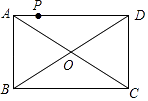

Answer 1

【答案】
【解析】解：解：连接OP，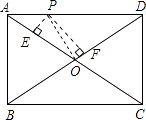
∵矩形的两条边AB、BC的长分别为6和8，
∴S矩形ABCD=ABBC=48，OA=OC，OB=OD，AC=BD=10，
∴OA=OD=5，
∴S△ACD= S矩形ABCD=24，
∴S△AOD= S△ACD=12，
∵S△AOD=S△AOP+S△DOP= OAPE+ ODPF= ×5×PE+ ×5×PF= （PE+PF）=12，
解得：PE+PF= ，
所以答案是
【考点精析】关于本题考查的点到直线的距离和矩形的性质，需要了解从直线外一点到这条直线的垂线段的长度叫做点到直线的距离；矩形的四个角都是直角，矩形的对角线相等才能得出正确答案．