题目内容
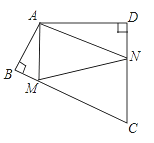
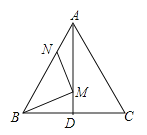
【题目】如图，在等边△ABC中，AB=6，N为线段AB上的任意一点，∠BAC的平分线交BC于点D，M是AD上的动点， 连结BM、MN，则BM+MN的最小值是 .
【答案】
【解析】
试题分析：
过点C作CN⊥AB于N，交AD于M,连接BM，根据两点之间线段最短和垂线段最短得出此时BM+MN最小，由于C和B关于AD对称，则BM+MN=CN,根据勾股定理求出CN，即可求出答案
试题解析：
解：过点C作CN⊥AB于N，交AD于M,连接BM，则BM+MN最小（根据两点之间线段最短和垂线段最短），由于C和B关于AD对称，则BM+MN=CN
∵等边
中，
平分
∴
∴AD是BC的垂直平分线（三线合一）
∴C和B关于直线AD对称
∴CM=BM
即BM+MN=CM+MN=CN
∵CN⊥AB
∴∠CNB=90o，CN是∠ACB的平分线，AN=BN（三线合一）
∵∠ACB=60°
∴∠BCN=30
∵AB=6
∴
在
中，由勾股定理得：
，
即
的最小值是
练习册系列答案
相关题目
【题目】随着车辆的增加，交通违规的现象越来越严重，交警对某雷达测速区检测到的一组汽车的时速数据进行整理，得到其频数及频率如表（未完成）：
时速数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | ___ |
50﹣60 | ___ | 0.39 |
60﹣70 | ___ | ___ |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
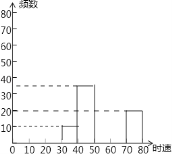
（1）请你把表中的数据填写完整；
（2）补全频数分布直方图；
（3）如果汽车时速超过60千米即为违章，则这次检测到的违章车辆共有 辆.
