题目内容
实数a、b、c满足
，则a2+b2-c2的平方根是________．
0
分析：根据任何数的绝对值，平方，算术平方根都是非负数，几个非负数的和等于0，则每个数等于0，即可得到关于a，b，c的式子求得a，b，c的值，进而求得代数式的值．
解答：根据题意得：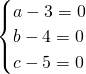
，
解得：
．
则a2+b2-c2=32+42-52=9+16-25=0．
∴a2+b2-c2的平方根是0．
故答案是：0．
点评：本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
分析：根据任何数的绝对值，平方，算术平方根都是非负数，几个非负数的和等于0，则每个数等于0，即可得到关于a，b，c的式子求得a，b，c的值，进而求得代数式的值．
解答：根据题意得：
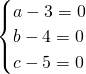，解得：
．则a2+b2-c2=32+42-52=9+16-25=0．
∴a2+b2-c2的平方根是0．
故答案是：0．
点评：本题考查了非负数的性质：几个非负数的和为0时，这几个非负数都为0．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
已知实数a、b、c满足a-b+c=0，那么关于x的方程ax2+bx+c=0一定有根（ ）
| A、x=1 | B、x=-1 | C、x=±1 | D、都不对 |
已知方程x2+（2k+1）x+k-1=0的两个实数根x1，x2满足x1-x2=4k-1，则实数k的值为（ ）
| A、1，0 | ||
| B、-3，0 | ||
C、1，-
| ||
D、1，-
|