题目内容
已知实数a、b、c满足a-b+c=0,那么关于x的方程ax2+bx+c=0一定有根( )
| A、x=1 | B、x=-1 | C、x=±1 | D、都不对 |
分析:由a-b+c=0得b=a+c代入方程ax2+bx+c=0中,可得方程的一个根是-1.
解答:解:∵a-b+c=0,
∴b=a+c,①
把①代入方程ax2+bx+c=0中,
ax2+(a+c)x+c=0,
ax2+ax+cx+c=0,
ax(x+1)+c(x+1)=0,
(x+1)(ax+c)=0,
∴x1=-1,x2=-
.
故本题选B.
∴b=a+c,①
把①代入方程ax2+bx+c=0中,
ax2+(a+c)x+c=0,
ax2+ax+cx+c=0,
ax(x+1)+c(x+1)=0,
(x+1)(ax+c)=0,
∴x1=-1,x2=-
| c |
| a |
故本题选B.
点评:本题考查的是一元二次方程的根,由题目中所给条件代入方程可以求出方程的两个根,其中有一个准确的根x=-1.

练习册系列答案
相关题目
 (2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式
(2013•菏泽)(1)已知m是方程x2-x-2=0的一个实数根,求代数式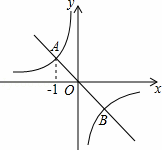
 (1)已知m是方程x2-x-2=0的一个实数根,求代数式
(1)已知m是方程x2-x-2=0的一个实数根,求代数式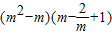 的值.
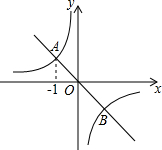
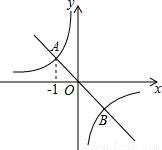
的值.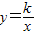 的图象交于A、B两点.
的图象交于A、B两点.