题目内容
如图,点P与点P′关于y轴对称,点P在双曲线y=
(k≠0)上,则此双曲线的解析式为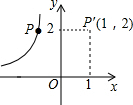
| k |
| x |
y=-
| 2 |
| x |
y=-
.| 2 |
| x |
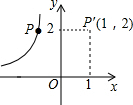
分析:首先根据关于y轴对称的点的坐标特点得到P点的坐标,再把P点坐标代入反比例函数的解析式即可算出k的值,进而得到反比例函数解析式.
解答: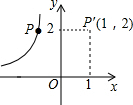 解:∵P′(1,2),点P与点P′关于y轴对称,
解:∵P′(1,2),点P与点P′关于y轴对称,
∴P(-1,2),
∵点P在双曲线y=
(k≠0)上,
∴k=-1×2=-2,
∴双曲线的解析式为y=-
,
故答案为:y=-
.
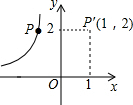 解:∵P′(1,2),点P与点P′关于y轴对称,
解:∵P′(1,2),点P与点P′关于y轴对称,∴P(-1,2),
∵点P在双曲线y=
| k |
| x |
∴k=-1×2=-2,
∴双曲线的解析式为y=-
| 2 |
| x |
故答案为:y=-
| 2 |
| x |
点评:此题主要考查了反比例函数图象上的点的坐标特点,以及关于y轴对称的点的坐标特点,关键是掌握关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.时间为t(s)(0<t<5).解答下列问题:
如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.时间为t(s)(0<t<5).解答下列问题: