题目内容
有4个正方形的边长分别为a，a+3，a+5，a+6，其面积之和记为M；另有4个正方形的边长分别为a+1，a+2，a+4，a+7，其面积之和记为N．则M，N的关系为M________N（填“＞”或“＜”或“=”）．
=
分析：利用完全平方公式求出每个正方形的面积，再求和，比较M，N的大小．
解答：∵M=a2+（a+3）2+（a+5）2+（a+6）2=a2+a2+6a+9+a2+10a+25+a2+12a+36=4a2+28a+70，
N=（a+1）2+（a+2）2+（a+4）2+（a+7）2=a2+2a+1+a2+4a+4+a2+8a+16+a2+14a+49=4a2+28a+70，
∴M=N．
故答案为：=．
点评：本题主要考查完全平方公式的应用，有一定难度，熟记公式是解题的关键．
分析：利用完全平方公式求出每个正方形的面积，再求和，比较M，N的大小．
解答：∵M=a2+（a+3）2+（a+5）2+（a+6）2=a2+a2+6a+9+a2+10a+25+a2+12a+36=4a2+28a+70，
N=（a+1）2+（a+2）2+（a+4）2+（a+7）2=a2+2a+1+a2+4a+4+a2+8a+16+a2+14a+49=4a2+28a+70，
∴M=N．
故答案为：=．
点评：本题主要考查完全平方公式的应用，有一定难度，熟记公式是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
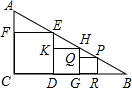如图，Rt△ABC中，∠C=90°，有三个正方形CDEF、DGHK、GRPQ，它们分别是△ACB、△EDB和△HGB的内接正方形，EF=10cm，HK=7cm，则第三个正方形的边长PQ的长（ ）
）
）
）