题目内容
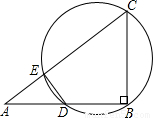
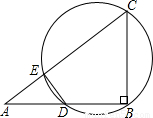
(2002•甘肃)(在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)(I)如图,在△ABC中,AB=4,BC=3,∠B=90°,点D在AB上运动,但与A、B不重合,过B、C、D三点的圆交AC于E,连接DE.
(1)设AD=x,CE=y,求y与x之间的函数关系式,并指出自变量x的取值范围;
(2)当AD长为关于x的方程2x2+(4m+1)x+2m=0的一个整数根时,求m的值.
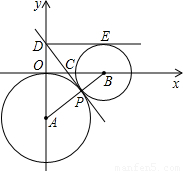
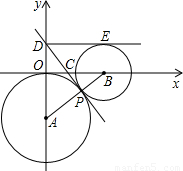
(II)如图,在直角坐标系xOy中,以点A(0,-3)为圆心作圆与x轴相切,⊙B与⊙A外切干点P,B点在x轴正半轴上,过P点作两圆的公切线DP交y轴于D,交x轴于C,
(1)设⊙A的半径为r1,⊙B的半径为r2,且r2=
 r1,求公切线DP的长及直线DP的函数解析式,
r1,求公切线DP的长及直线DP的函数解析式,(2)若⊙A的位置、大小不变,点B在X轴正半轴上移动,⊙B与⊙A始终外切.过D作⊙B的切线DE,E为切点.当DE=4时,B点在什么位置?从解答中能发现什么?
【答案】分析:(Ⅰ)(1)可先在直角三角形ABC中,求出AC的长,然后根据相似三角形ADE和ABC,得出关于AE,AB,AD,AC的比例关系式,用x表示出AE,然后根据AE+EC=AC即可得出关于x,y的函数关系式;
(2)观察方程,可先用十字相乘法解方程,用m表示出方程的根,然后根据方程的根为整数,来判断m的取值.
(Ⅱ)(1)由于三角形ADP和ABO全等(一个公共角,一组直角,AO=AP),因此要求DP的长,就是求出OB的长,已知了A的坐标,也就知道了⊙A的半径长,根据⊙A,⊙B的半径的比例关系即可求出BP的长,那么就知道了AB的长,可在直角三角形AOB中得出OB的值,也就求出了DP的长.求DP所在的直线的解析式,就要知道D,C两点的坐标,关键是求OD,OC,因为三角形ADP和ABO全等,那么求出了AB的长,也就知道了AD的长,根据OD=AD-OA,即可得出D的坐标,根据相似△DOC和△BOA,可求出OC的长,那么知道了D,C的坐标后,可用待定系数法求出DP所在直线的解析式;
(2)很显然,四边形OBED是矩形,由此可以求出B点的坐标应该是(0,4).
解答:(Ⅰ)解:(1)在△ABC中,∠B=90°,AB=4,BC=3,
∴AC=5,
∵四边形DBCE为圆的内接四边形,
∴∠AED=∠B,又∠A=∠A,
∴△ADE∽△ACB,
∴AE:AB=AD:AC,
∴AE=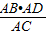 =
= x,
x,
由CE=AC-AE得y=5- x=-
x=- x+5,
x+5,
∵点D在AB上运动,且与A,B不重合,AB=4,
∴自变量x的取值范围是0<x<4;
(2)∵2x2+(4m+1)x+2m=0,
∴(x+2m)(2x+1)=0,
∴x=-2m,x=- ,
,
∵x=- 是分数.
是分数.
∴整数根为-2m,即AD=-2m,
∵0<x<4,即0<AD<4,
∴满足0<AD<4的正数为1,2,3,
当AD=-2m=1时,m=- ;
;
当AD=-2m=2时,m=-1;
当AD=-2m=3时,m=- .
.
∵方程2x2+(4m+1)x+2m的判别式为△=(4m+1)2-16m=(4m-1)2,
对任何实数m恒有(4m-1)2≥0,
∴所求的值为- ,-1和-
,-1和- .
.
(Ⅱ)解:(1)∵A(0,-3),
∴AO=AP=3,
又r2= r1,即BP=
r1,即BP= AP=2,
AP=2,
∴AB=5,
∴BO=4.
又Rt△AOB∽Rt△CPB,得: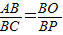 ,
,
∴BC=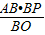 =
= ,OC=4-
,OC=4- =
= .
.
∴点C的坐标是C( ,0)
,0)
∵Rt△APD≌Rt△AOB,
∴AD=AB=5,PD=BO=4
设点PD的解析式为y=kx+b,则有:
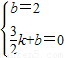 ,
,
得k=- ,b=2,
,b=2,
∴直线PD的解析式是y=- x+2;
x+2;
(2)点B的坐标为(4,0),
可以看出,四边形OBED是矩形.
点评:本题主要考查了相似三角形的判定和性质,全等三角形的判定和性质以及圆与圆的位置关系等知识点,也考查了利用待定系数法确定函数的解析式,综合性比较强.
(2)观察方程,可先用十字相乘法解方程,用m表示出方程的根,然后根据方程的根为整数,来判断m的取值.
(Ⅱ)(1)由于三角形ADP和ABO全等(一个公共角,一组直角,AO=AP),因此要求DP的长,就是求出OB的长,已知了A的坐标,也就知道了⊙A的半径长,根据⊙A,⊙B的半径的比例关系即可求出BP的长,那么就知道了AB的长,可在直角三角形AOB中得出OB的值,也就求出了DP的长.求DP所在的直线的解析式,就要知道D,C两点的坐标,关键是求OD,OC,因为三角形ADP和ABO全等,那么求出了AB的长,也就知道了AD的长,根据OD=AD-OA,即可得出D的坐标,根据相似△DOC和△BOA,可求出OC的长,那么知道了D,C的坐标后,可用待定系数法求出DP所在直线的解析式;
(2)很显然,四边形OBED是矩形,由此可以求出B点的坐标应该是(0,4).
解答:(Ⅰ)解:(1)在△ABC中,∠B=90°,AB=4,BC=3,
∴AC=5,
∵四边形DBCE为圆的内接四边形,
∴∠AED=∠B,又∠A=∠A,
∴△ADE∽△ACB,
∴AE:AB=AD:AC,
∴AE=
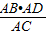 =
= x,
x,由CE=AC-AE得y=5-
 x=-
x=- x+5,
x+5,∵点D在AB上运动,且与A,B不重合,AB=4,
∴自变量x的取值范围是0<x<4;
(2)∵2x2+(4m+1)x+2m=0,
∴(x+2m)(2x+1)=0,
∴x=-2m,x=-
 ,
,∵x=-
 是分数.
是分数.∴整数根为-2m,即AD=-2m,
∵0<x<4,即0<AD<4,
∴满足0<AD<4的正数为1,2,3,
当AD=-2m=1时,m=-
 ;
;当AD=-2m=2时,m=-1;
当AD=-2m=3时,m=-
 .
.∵方程2x2+(4m+1)x+2m的判别式为△=(4m+1)2-16m=(4m-1)2,
对任何实数m恒有(4m-1)2≥0,
∴所求的值为-
 ,-1和-
,-1和- .
.(Ⅱ)解:(1)∵A(0,-3),
∴AO=AP=3,
又r2=
 r1,即BP=
r1,即BP= AP=2,
AP=2,∴AB=5,
∴BO=4.
又Rt△AOB∽Rt△CPB,得:
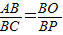 ,
,∴BC=
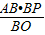 =
= ,OC=4-
,OC=4- =
= .
.∴点C的坐标是C(
 ,0)
,0)∵Rt△APD≌Rt△AOB,
∴AD=AB=5,PD=BO=4
设点PD的解析式为y=kx+b,则有:
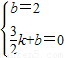 ,
,得k=-
 ,b=2,
,b=2,∴直线PD的解析式是y=-
 x+2;
x+2;(2)点B的坐标为(4,0),
可以看出,四边形OBED是矩形.
点评:本题主要考查了相似三角形的判定和性质,全等三角形的判定和性质以及圆与圆的位置关系等知识点,也考查了利用待定系数法确定函数的解析式,综合性比较强.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 r1,求公切线DP的长及直线DP的函数解析式,
r1,求公切线DP的长及直线DP的函数解析式,

 r1,求公切线DP的长及直线DP的函数解析式,
r1,求公切线DP的长及直线DP的函数解析式,