题目内容
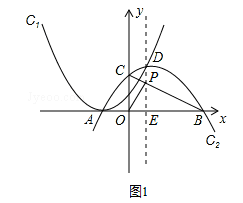
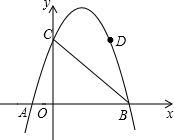
如图,抛物线C1:y=(x+m)2(m为常数,m>0),平移抛物线y=﹣x2,使其顶点D在抛物线C1位于y轴右侧的图象上,得到抛物线C2.抛物线C2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,设点D的横坐标为a.
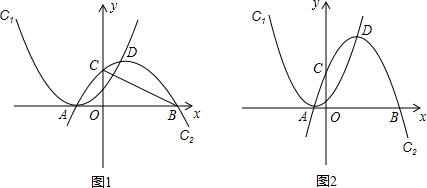
(1)如图1,若m= .
.
①当OC=2时,求抛物线C2的解析式;
②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
(2)如图2,当OB=2 ﹣m(0<m<
﹣m(0<m< )时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).

(1)如图1,若m=
 .
.①当OC=2时,求抛物线C2的解析式;
②是否存在a,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP=BP?若存在,求出a的值;若不存在,请说明理由;
(2)如图2,当OB=2
 ﹣m(0<m<
﹣m(0<m< )时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).
)时,请直接写出到△ABD的三边所在直线的距离相等的所有点的坐标(用含m的式子表示).(1) ①y=﹣x2+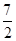 x+2.②
x+2.②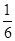 .(2)P1(
.(2)P1( ﹣m,1),P2(
﹣m,1),P2( ﹣m,﹣3),P3(﹣
﹣m,﹣3),P3(﹣ ﹣m,3),P4(3
﹣m,3),P4(3 ﹣m,3).
﹣m,3).
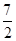 x+2.②
x+2.②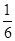 .(2)P1(
.(2)P1( ﹣m,1),P2(
﹣m,1),P2( ﹣m,﹣3),P3(﹣
﹣m,﹣3),P3(﹣ ﹣m,3),P4(3
﹣m,3),P4(3 ﹣m,3).
﹣m,3).试题分析:(1)①首先写出平移后抛物线C2的解析式(含有未知数a),然后利用点C(0,2)在C2上,求出抛物线C2的解析式;
②认真审题,题中条件“AP=BP”意味着点P在对称轴上,“点B与点C到直线OP的距离之和最大”意味着OP⊥BC.画出图形,如图1所示,利用三角函数(或相似),求出a的值;
(2)解题要点有3个:
i)判定△ABD为等边三角形;
ii)理论依据是角平分线的性质,即角平分线上的点到角两边的距离相等;
iii)满足条件的点有4个,即△ABD形内1个(内心),形外3个.不要漏解.
试题解析:(1)当m=
 时,抛物线C1:y=(x+
时,抛物线C1:y=(x+ )2.
)2.∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,
∴D(a,(a+
 )2).
)2).∴抛物线C2:y=﹣(x﹣a)2+(a+
 )2(I).
)2(I).①∵OC=2,∴C(0,2).
∵点C在抛物线C2上,
∴﹣(0﹣a)2+(a+
 )2=2,
)2=2,解得:a=
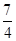 ,代入(I)式,
,代入(I)式,得抛物线C2的解析式为:y=﹣x2+
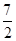 x+2.
x+2.②在(I)式中,
令y=0,即:﹣(x﹣a)2+(a+
 )2=0,解得x=2a+
)2=0,解得x=2a+ 或x=﹣
或x=﹣ ,∴B(2a+,0);
,∴B(2a+,0);令x=0,得:y=a+
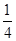 ,∴C(0,a+
,∴C(0,a+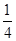 ).
).设直线BC的解析式为y=kx+b,则有:
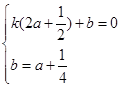 ,解得
,解得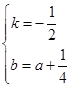 ,
,∴直线BC的解析式为:y=﹣
 x+(a+
x+(a+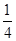 ).
).假设存在满足条件的a值.
∵AP=BP,
∴点P在AB的垂直平分线上,即点P在C2的对称轴上;
∵点B与点C到直线OP的距离之和≤BC,只有OP⊥BC时等号成立,
∴OP⊥BC.
如图1所示,设C2对称轴x=a(a>0)与BC交于点P,与x轴交于点E,
则OP⊥BC,OE=a.
∵点P在直线BC上,
∴P(a,
 a+
a+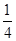 ),PE=
),PE= a+
a+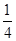 .
.∵tan∠EOP=tan∠BCO=
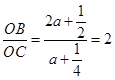 ,
,∴
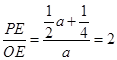 ,
,解得:a=
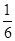 .
.∴存在a=
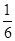 ,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP="BP"
,使得线段BC上有一点P,满足点B与点C到直线OP的距离之和最大且AP="BP" (3)∵抛物线C2的顶点D在抛物线C1上,且横坐标为a,
∴D(a,(a+m)2).
∴抛物线C2:y=﹣(x﹣a)2+(a+m)2.
令y=0,即﹣(x﹣a)2+(a+m)2=0,解得:x1=2a+m,x2=﹣m,∴B(2a+m,0).
∵OB=2
 ﹣m,
﹣m,∴2a+m=2
 ﹣m,
﹣m,∴a=
 ﹣m.
﹣m.∴D(
 ﹣m,3).
﹣m,3).AB=OB+OA=2
 ﹣m+m=2
﹣m+m=2 .
.如图2所示,设对称轴与x轴交于点E,则DE=3,BE=AB=
 ,OE=OB﹣BE=
,OE=OB﹣BE= ﹣m.
﹣m.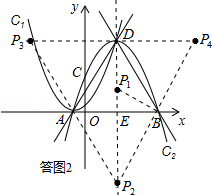
∵tan∠ABD=
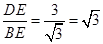 ,
,∴∠ABD=60°.
又∵AD=BD,∴△ABD为等边三角形.
作∠ABD的平分线,交DE于点P1,则P1E=BE•tan30°=
 ×
×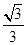 =1,
=1,∴P1(
 ﹣m,1);
﹣m,1);在△ABD形外,依次作各个外角的平分线,它们相交于点P2、P3、P4.
在Rt△BEP2中,P2E=BE•tan60°=
 •
• =3,
=3,∴P2(
 ﹣m,﹣3);
﹣m,﹣3);易知△ADP3、△BDP4均为等边三角形,∴DP3=DP4=AB=2
 ,且P3P4∥x轴.
,且P3P4∥x轴.∴P3(﹣
 ﹣m,3)、P4(3
﹣m,3)、P4(3 ﹣m,3).
﹣m,3).综上所述,到△ABD的三边所在直线的距离相等的所有点有4个,
其坐标为:P1(
 ﹣m,1),P2(
﹣m,1),P2( ﹣m,﹣3),P3(﹣
﹣m,﹣3),P3(﹣ ﹣m,3),P4(3
﹣m,3),P4(3 ﹣m,3).
﹣m,3).【考点】二次函数综合题.

练习册系列答案
相关题目
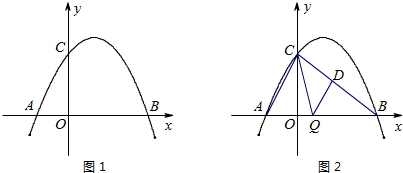
 的横坐标,将它所对的面的数字作为点
的横坐标,将它所对的面的数字作为点 与
与 轴所围成的区域内(不含边界)的概率是 .
轴所围成的区域内(不含边界)的概率是 .

 =
= ,当
,当 <
< <
< 时,
时, 


 ,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
,BC=6,点E为对角线AC的中点,点P在边BC上,连接PE、PA.当点P在BC上运动时,设BP=x,△APE的周长为y,下列图象中,能表示y与x的函数关系的图象大致是( )
 B.
B. C.
C. D.
D.