题目内容
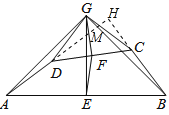
【题目】如下图1,在四边形ABCD中,点E、F分别是AB、CD的中点.过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连结GA、GB、GC、GD、EF,若∠AGD=∠BGC.

(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:本题是相似形综合题目,考查了线段垂直平分线的性质、全等三角形的判定与性质、相似三角形的判定与性质、三角函数等知识;本题难度较大,综合性强,特别是(3)中,需要通过作辅助线综合运用(1)(2)的结论和三角函数才能得出结果.
(2)先证出∠AGB=∠DGC,由![]() =
=![]() ,证出△AGB∽△DGC,得出比例式
,证出△AGB∽△DGC,得出比例式![]() =
=![]() ,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
,再证出∠AGD=∠EGF,即可得出△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,则AH⊥BH,由△AGD≌△BGC,得出∠GAD=∠GBC,再求出∠AGE=∠AHB=90°,得出∠AGE=![]() ∠AGB=45°,求出
∠AGB=45°,求出![]() =
=![]() ,由△AGD∽△EGF,即可得出
,由△AGD∽△EGF,即可得出![]() 的值即可.
的值即可.
试题解析:(1)∵GE是AB的垂直平分线,
∴GA=GB,
同理:GD=GC,
在△AGD和△BGC中,
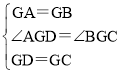 ,
,
∴△AGD≌△BGC(SAS),
∴AD=BC;
(2)∵∠AGD=∠BGC,
∴∠AGB=∠DGC,
在△AGB和△DGC中,![]() =
=![]() ,
,
∴△AGB∽△DGC,
∴![]() =
=![]() ,
,
又∵∠AGE=∠DGF,
∴∠AGD=∠EGF,
∴△AGD∽△EGF;
(3)延长AD交GB于点M,交BC的延长线于点H,如图所示,则AH⊥BH,
∵△AGD≌△BGC,
∴∠GAD=∠GBC,
在△GAM和△HBM中,∠GAD=∠GBC,∠GMA=∠HMB,
∴∠AGB=∠AHB=90°,
∴∠AGE=![]() ∠AGB=45°,
∠AGB=45°,
∴![]() =
=![]() ,
,
又∵△AGD∽△EGF,
∴![]() =
=![]() =
=![]() .
.