题目内容
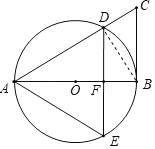
【题目】如图，AB是
的直径，点C是外一点，连接AC，BC，AC与交于点D，弦DE与直径AB交于点F，
．
求证：BC是的切线；
若
，
，
，求CD的长．
【答案】(1)见解析；
．
【解析】
（1）连接BD，根据圆周角定理得到∠BAE=∠BDE，推出∠C=∠ABD，由AB是⊙O的直径，得到∠ADB=90°，推出AB⊥BC，于是得到结论；
（2）根据垂径定理得到
，等量代换得到
，求得∠ABD=2∠DAB，解直角三角形即可得到结论．
（1）连接BD，则∠BAE=∠BDE．
∵∠AFE=∠DFB，∴∠E=∠ABD．
∵∠C=∠E，∴∠C=∠ABD．
∵AB是⊙O的直径，∴∠ADB=90°，∴∠BDC=90°，∴∠C+∠CBD=90°，∴∠ABD+∠CBD=90°，∴AB⊥BC，∴BC是⊙O的切线；
（2）∵AB是⊙O的直径，DE⊥AB，∴
，∴，∴∠ABD=2∠DAB，∴∠BAC=30°，∠ABD=60°，∴∠C=60°，∴∠CBD=30°．
∵AB=2
，∴BC
AB=2，∴CD
BC=1．
练习册系列答案
相关题目
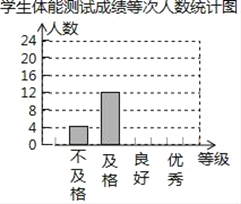
【题目】某校为了解学生体质情况，从各年级随机抽取部分学生进行体能测试，每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级，统计员在将测试数据绘制成图表时发现，优秀漏统计4人，良好漏统计6人，于是及时更正，从而形成如图图表，请按正确数据解答下列各题：
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 | 8 |
|
良好 | 16 |
|
及格 | 12 |
|
不及格 | 4 |
|
合计 | 40 |
|
（1）填写统计表；
（2）根据调整后数据，补全条形统计图；
（3）若该校共有学生1500人，请你估算出该校体能测试等级为“优秀”的人数．
