题目内容
在第29届北京奥运会开幕前,某商场抓住商机,以单价40元的价格购进一批衬衫,然后加工印上“中国印”图案,再以单价50元出售,每周可售出500件.经调查发现,售价每提高1元,销售量相应减少10件.
(1)请写出每月售出衬衫的利润y(元)与每件衬衫涨价x(元)的函数关系式;
(2)每件衬衫的售价应为多少元时,每周销售利润最大?最大的周销售利润是多少?
(3)请你通过(1)中的函数关系式及其大致图象分析该商场衬衫的销售单价在什么范围内时,商场获得的周销售利润不低于8000元.
(1)请写出每月售出衬衫的利润y(元)与每件衬衫涨价x(元)的函数关系式;
(2)每件衬衫的售价应为多少元时,每周销售利润最大?最大的周销售利润是多少?
(3)请你通过(1)中的函数关系式及其大致图象分析该商场衬衫的销售单价在什么范围内时,商场获得的周销售利润不低于8000元.
分析:(1)根据每月售出衬衫的利润=每件的利润×每周的销售量得到y=(50+x-40)(500-10x),整理即可;
(2)把y=-10(x-20)2+9000配成二次函数的顶点式,然后根据二次函数的性质即可得到答案;
(3)先计算出y=8000时所对应的x的值,然后画出函数的大致图象,再根据图象回答即可.
(2)把y=-10(x-20)2+9000配成二次函数的顶点式,然后根据二次函数的性质即可得到答案;
(3)先计算出y=8000时所对应的x的值,然后画出函数的大致图象,再根据图象回答即可.
解答:解:(1)y=(50+x-40)(500-10x)
=-10x2+400x+5000,
(2)y=-10x2+400x+5000
=-10(x-20)2+9000,
∵a=-10<0,
∴x=20时,y有最大值9000,
即销售单价定为70元时,每周销售利润最大,最大的周销售利润是9000元;
(3)令y=8000,则-10(x-20)2+9000=8000,解得x1=10,x2=30.
函数的大致图象为: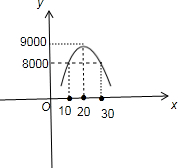
观察图象当10≤x≤30时,y不低于8000.
所以当销售单价不小于60元而不大于80元时,商场获得的周销售利润不低于8000元.
=-10x2+400x+5000,
(2)y=-10x2+400x+5000
=-10(x-20)2+9000,
∵a=-10<0,
∴x=20时,y有最大值9000,
即销售单价定为70元时,每周销售利润最大,最大的周销售利润是9000元;
(3)令y=8000,则-10(x-20)2+9000=8000,解得x1=10,x2=30.
函数的大致图象为:

观察图象当10≤x≤30时,y不低于8000.
所以当销售单价不小于60元而不大于80元时,商场获得的周销售利润不低于8000元.
点评:本题考查了二次函数的应用:先得到二次函数的顶点式y=a(x-h)2+k,当a<0,x=h时,y有最大值k;当a<0,x=h时,y有最小值k.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
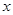 元,每周销量为
元,每周销量为 件。
件。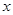 元,每周销量为
元,每周销量为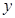 件。
件。