题目内容
在第29届北京奥运会开幕前,某商场抓住商机,以单价40元的价格购进一批衬衫,然后加工印上“中国印”图案,再以单价50元出售,每周可售出500件.经调查发现,售价每提高1元,销售量相应减少10件.设每件涨价x元,每周销量为y件.
(1)求y与x的函数关系式;
(2)如何定价才能使每周的利润为8000元且使得这种衬衫每周的销量较大?
解:(1)由题意可知:y=-10x+b,当x=50时,y=500,求得b=500,
∴y=500-10x;
(2)(x+10)(500-10x)=8000
∴x1=10,x2=30
∵要求每周的销量较大
∴x=10
∴当定价60元时,才能使每周的利润为8000元
且使得这种衬衫每周的销量较大.
分析:(1)从题意可知,每件涨价x元与每周销量为y件之间存在着一次函数的关系.每提高1元,销售量相应减少10件,说明变化率为-10,从而可以列出式子y=-10x+b,当x=0时,y=500,从而得到b的值,从而得到关系y=500-10x;
(2)因为利润=销售量×每件衬衫的利润,每件衬衫的利润=售价-成本,由此可以列出式子8000=y×(x+10),由(1)中y与x的关系y=500-10x,可以求得x的值,当销量最大时,y最大,x取小值.
点评:解答一次函数的应用问题中,一定要读懂题意之后才开始做题,找出其中之间的关系.
∴y=500-10x;
(2)(x+10)(500-10x)=8000
∴x1=10,x2=30
∵要求每周的销量较大
∴x=10
∴当定价60元时,才能使每周的利润为8000元
且使得这种衬衫每周的销量较大.
分析:(1)从题意可知,每件涨价x元与每周销量为y件之间存在着一次函数的关系.每提高1元,销售量相应减少10件,说明变化率为-10,从而可以列出式子y=-10x+b,当x=0时,y=500,从而得到b的值,从而得到关系y=500-10x;
(2)因为利润=销售量×每件衬衫的利润,每件衬衫的利润=售价-成本,由此可以列出式子8000=y×(x+10),由(1)中y与x的关系y=500-10x,可以求得x的值,当销量最大时,y最大,x取小值.
点评:解答一次函数的应用问题中,一定要读懂题意之后才开始做题,找出其中之间的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
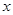 元,每周销量为
元,每周销量为 件。
件。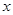 元,每周销量为
元,每周销量为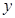 件。
件。