Question

【题目】如图4，已知AB为半圆O的直径，BC⊥AB于点B，且BC＝AB，D为半圆上一点，连结BD并延长交半圆O的切线AE于点E.

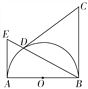
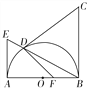
图4①　　 　图4②

(1)如图①，若CD＝CB，求证：CD为半圆O的切线；

(2)如图②，若点F在OB上，且FD⊥CD，求的值．

Answer 1

【答案】(1)见解析；(2)1.

【解析】(1)、连接DO，CO，易证△CDO≌△CBO，即可解题；(2)、连接AD，易证△ADF∽△BDC和△ADE∽△BDA，根据相似三角形对应边比例相等的性质即可解题．

(1)证明：如答图①，连结DO，CO，

∵BC⊥AB，∴∠ABC＝90°，在△CDO与△CBO中，

∴△CDO≌△CBO，∴∠CDO＝∠CBO＝90°， ∴OD⊥CD，∴CD为半圆O的切线；

(2)如答图②，连结AD，∵AB是直径，∴∠ADB＝90°，

∴∠ADF＋∠BDF＝90°，∠DAB＋∠DBA＝90°，

∵∠BDF＋∠BDC＝90°，∠CBD＋∠DBA＝90°，∴∠ADF＝∠BDC，∠DAB＝∠CBD，

∴△ADF∽△BDC，∴＝， ∵∠DAE＋∠DAB＝90°，∠E＋∠DAE＝90°，

∴∠E＝∠DAB， ∵在△ADE和△BDA中，

∴△ADE∽△BDA，∴＝，∴＝，即＝， ∵AB＝BC，∴＝1.