题目内容
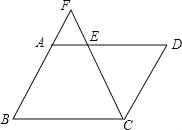
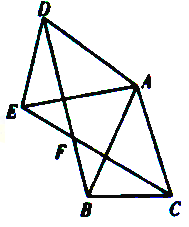
【题目】(2016贵州省毕节市第25题)如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:![]() ;
;
(2)若AB=2,![]() ,当四边形ADFC是菱形时,求BF的长。
,当四边形ADFC是菱形时,求BF的长。
【答案】(1)、证明过程见解析;(2)、BF=2![]() -2
-2
【解析】
(2)试题分析:(1)、根据△ABC≌△ADE得出AE=AD,∠BAC=∠DAE,从而得出∠CAE=∠DAB,根据SAS判定定理得出三角形全等;(2)、根据菱形的性质得出∠DBA=∠BAC=45°,根据AB=AD得出△ABD是直角边长为2的等腰直角三角形,从而得出BD=2![]() ,根据菱形的性质得出AD=DF=FC=AC=AB=2,最后根据BF=BD-DF求出答案.
,根据菱形的性质得出AD=DF=FC=AC=AB=2,最后根据BF=BD-DF求出答案.
试题解析:(1)、∵△ABC≌△ADE且AB=AC ∴AE=AD,AB=AC
∠BAC+∠BAE=∠DAE+∠BAE ∴∠CAE=∠DAB ∴△AEC≌△ADB
(3)、∵四边形ADFC是菱形且∠BAC=45° ∴∠DBA=∠BAC=45° 由(1)得AB=AD
∴∠DBA=∠BDA=45° ∴△ABD是直角边长为2的等腰直角三角形 ∴BD=2![]()
又∵四边形ADFC是菱形 ∴AD=DF=FC=AC=AB=2 ∴BF=BD-DF=2![]() -2
-2

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目