题目内容
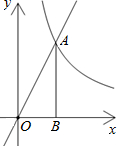 已知图中的曲线是反比例函数y=
已知图中的曲线是反比例函数y=| m-5 |
| x |
(1)这个反比例函数图象的另一支在第几象限?常数m的取值范围是什么?
(2)若该函数的图象与正比例函数y=2x的图象在第一象限内的交点为A,过A点作x轴的垂线,垂足为B,当△OAB的面积为4时,求此反比例函数的解析式;
(3)设直线y=2x与反比例函数y=
| m-5 |
| x |
分析:(1)根据反比例函数的性质可求得比例函数的图象分布在第一、第三象限,所以m-5>0即可求解;
(2)点A的横坐标为a,根据点A在y=2x上,可表示出A点纵坐标为2a,点B的坐标为(a,0),根据三角形面积公式可得
a•2a=4,算出a的值,进而得到A点坐标,再利用待定系数法可求出反比例函数解析式;
(3)首先画出图象,根据A点坐标可得到C点坐标,再根据三角形的面积公式计算即可.
(2)点A的横坐标为a,根据点A在y=2x上,可表示出A点纵坐标为2a,点B的坐标为(a,0),根据三角形面积公式可得
| 1 |
| 2 |
(3)首先画出图象,根据A点坐标可得到C点坐标,再根据三角形的面积公式计算即可.
解答:解:(1)这个反比例函数图象的另一支在第三象限,
∵这个反比例函数y=
的图象分布在第一、第三象限,
∴m-5>0,
解得m>5;
(2)设点A的横坐标为a,
∵点A在y=2x上,
∴点A的纵坐标为2a,
∵AB⊥x轴,
∴点B的坐标为(a,0)
∵S△OAB=4,
∴
a•2a=4,
解得a=2或-2(负值舍去),
∴点A的坐标为(2,4),
又∵点A在反比例函数y=
的图象上,
∴4=
,即m-5=8.
∴反比例函数的解析式为y=
;
(3)∵A、C两点是正比例函数y=2x与反比例函数图象的交点,
∴A、C两点关于原点对称,
∵点A的坐标为(2,4),
∴C(-2,-4),
S=S△BCO+S△BOA=
×BO×4+
×BO×4=
×2×4+
×2×4=8.
∵这个反比例函数y=
| m-5 |
| x |
∴m-5>0,
解得m>5;
(2)设点A的横坐标为a,
∵点A在y=2x上,
∴点A的纵坐标为2a,
∵AB⊥x轴,
∴点B的坐标为(a,0)
∵S△OAB=4,
∴
| 1 |
| 2 |
解得a=2或-2(负值舍去),
∴点A的坐标为(2,4),

又∵点A在反比例函数y=
| m-5 |
| x |
∴4=
| m-5 |
| 2 |
∴反比例函数的解析式为y=
| 8 |
| x |
(3)∵A、C两点是正比例函数y=2x与反比例函数图象的交点,
∴A、C两点关于原点对称,
∵点A的坐标为(2,4),
∴C(-2,-4),
S=S△BCO+S△BOA=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题主要考查了反比例函数的性质,三角形的面积公式,解决问题的关键是根据正比例函数结合三角形ABO的面积求出A点坐标,掌握正比例函数与反比函数图象的交点关于原点对称.

练习册系列答案
相关题目
 已知图中的曲线是反比例函数
已知图中的曲线是反比例函数
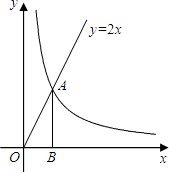 已知图中的曲线是反比例函数
已知图中的曲线是反比例函数