题目内容
阅读理解题:解不等式
| 2ax |
| 3 |
| 3 |
| 2 |
第一步:4ax-9≥6①
第二步:4ax≥15②
第三步:x≥
| 15 |
| 4a |
问:(1)上述解题过程中的第一步叫做
(2)上述解题过程中从哪一步开始出现错误?请写出该步的代号:
(3)错误的原因为
(4)本题正确的结论是什么?
分析:这是一个含有字母系数的不等式,仔细观察
-
≥1,通过去分母、去括号、移项并合并、再分情况讨论,系数化为1,求得解集.
| 2ax |
| 3 |
| 3 |
| 2 |
解答:解:(1)去分母,不等式的性质2;
(2)③;
(3)没有确定a的符号,若a≤0,则③不成立;
(4)应分a>0,a<0,a=0三种情况.
当a>0时,x≥
;
当a<0时,x≤
;
当a=0时,无解.
故填空答案为:去分母,不等式的性质2;③;没有确定a的符号,若a≤0,则③不成立.
(2)③;
(3)没有确定a的符号,若a≤0,则③不成立;
(4)应分a>0,a<0,a=0三种情况.
当a>0时,x≥
| 15 |
| 4a |
当a<0时,x≤
| 15 |
| 4a |
当a=0时,无解.
故填空答案为:去分母,不等式的性质2;③;没有确定a的符号,若a≤0,则③不成立.
点评:本题考查了不等式的性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.注意分三种情况讨论.
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.注意分三种情况讨论.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
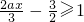 .
.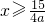 ③
③