题目内容
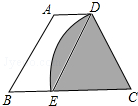（2013•历城区三模）如图，等腰梯形ABCD中，AD∥BC，以点C为圆心，CD为半径的弧与BC交于点E，四边形ABED是平行四边形，AB=3，则扇形CDE（阴影部分）的面积是| 3 |
| 2 |
| 3 |
| 2 |
分析：根据题意证得△DEC为等边三角形，则∠C=60°；然后根据扇形面积公式S=
可以求得扇形CDE（阴影部分）的面积．
| nπR2 |
| 360 |
解答：解：∵四边形ABCD是等腰梯形，且AD∥BC，
∴AB=CD；
又∵四边形ABED是平行四边形，
∴AB=DE（平行四边形的对边相等），
∴DE=DC=AB=3；
∵CE=CD，
∴CE=CD=DE=3，
∴∠C=60°，
∴S扇形CDE（阴影部分）=
=
π．
故答案为：
π．
∴AB=CD；
又∵四边形ABED是平行四边形，
∴AB=DE（平行四边形的对边相等），
∴DE=DC=AB=3；
∵CE=CD，
∴CE=CD=DE=3，
∴∠C=60°，
∴S扇形CDE（阴影部分）=
| 60π32 |
| 360 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题考查的是等腰梯形的性质，涉及到了平行四边形的性质、等边三角形的判定与性质以及扇形面积的计算．根据已知条件证得△DEC为等边三角形是解题的关键．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
（2013•历城区三模）如图，已知直角梯形ABCD中，AD∥BC，∠BAD=90°，AD=2，AB=4，BC=5，点P为AB边上一动点，连接PC、PD，若△PCD为直角三角形，则满足条件的点P有（ ）
（2013•历城区三模）如图，在斜边长为1的等腰直角三角形OAB中，作内接正方形A1B1D1C1；在等腰直角三角形OA1B1中作内接正方形A2B2D2C2；在等腰直角三角形OA2B2中作内接正方形A3B3D3C3；…；依次做下去，则第n个正方形AnBnDnCn的边长是
（2013•历城区三模）如图，已知点（1，2）在函数y=