题目内容
【题目】已知:如图,AB∥CD,∠B=∠D.点EF分别在AB、CD上.连接AC,分别交DE、BF于G、H.求证:∠1+∠2=180°
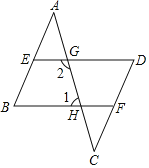
证明:∵AB∥CD,
∴∠B=_____._____
又∵∠B=∠D,
∴_____=_____.(等量代换)
∴_____∥_____._____
∴∠l+∠2=180°._____
【答案】∠BFC 两直线平行,内错角相等 ∠D ∠BFC DE BF 同位角相等,两直线平行 两直线平行,同旁内角互补
【解析】
根据平行线的性质结合已知得到∠D=∠BFC,证明DE∥BF,利用平行线的性质得出结论.
证明:∵AB∥CD,
∴∠B=∠BFC.(两直线平行,内错角相等),
又∵∠B=∠D,
∴∠D=∠BFC.(等量代换)
∴DE∥BF.(同位角相等,两直线平行),
∴∠l+∠2=180°.(两直线平行,同旁内角互补).
故答案为:∠BFC;两直线平行,内错角相等;∠D;∠BFC;DE;BF;同位角相等,两直线平行;两直线平行,同旁内角互补.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目