题目内容
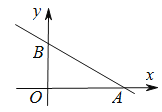
【题目】如图,已知直线![]() 分别与x、y轴交于点A和B.
分别与x、y轴交于点A和B.
(1)求点A、B的坐标;
(2)求原点O到直线的距离;
(3)若圆M的半径为2,圆心M在y轴上,当圆M与直线相切时,求点M的坐标.
【答案】(1)A点坐标为(4,0),B点坐标(0,3);
(2)原点O到直线l的距离为![]() .
.
(3)点M的坐标为M(0, ![]() )或 M(0,
)或 M(0, ![]() ).
).
【解析】试题分析:(1)对于直线解析式,分别令x与y为0,求出y与x的值,即可确定出A与B的坐标;
(2)利用点到直线的距离公式求出原点O到直线l的距离即可;
(3)设M坐标为(0,m),确定出OM,分两种情况考虑:若M在B点下边时,BM=3-m;若M在B点上边时,BM=m-3,利用相似三角形对应边成比例求出m的值,即可确定出M的坐标;
试题解析:
解(1)∵当x=0时,y=3 ,
∴B点坐标(0,3) .
∵当y=0时,有![]() ,解得x=4.
,解得x=4.
∴A点坐标为(4,0).
(2)如答图1,过点O作OC⊥AB于点C,则OC长为原点O到直线l的距离.
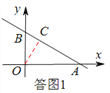
在Rt△BOA中,OA=4,0B=3,由勾股定理可得AB=5,
∵![]() ,
,
∴![]() .
.
∴原点O到直线l的距离为![]() .
.
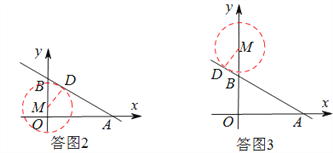
(3)如答图2,3,过点M作MD⊥AB交AB于点D,则当圆M与直线 l相切时,MD=2,
在△BOA和△BDM中,∵∠OBA=∠DBM,∠BOA=∠BDM,∴△BOA∽△BDM.
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
∴![]() 或
或![]() .
.
∴点M的坐标为M(0, ![]() )或 M(0,
)或 M(0, ![]() ).
).

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目