题目内容
如图,在直角坐标系中,点P(3,3),两坐标轴的正半轴上有M,N两点,且
SinP=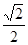 ,则△MON的周长等于__________
,则△MON的周长等于__________
SinP=
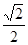 ,则△MON的周长等于__________
,则△MON的周长等于__________
6
作PA⊥y轴,PB⊥x轴.在x轴上截取BD=OA=OB=3,再截取DC=OM,可以证明△PMN≌△PCN,即可证得:△MON的周长=OM+ON+MN=CD+ON+CN=OD,即可求解.

解:作PA⊥y轴,PB⊥x轴.在x轴上截取BD=OA=OB=3,再截取DC=OM.
因为PA=PB=BD=OA=OB=3
故:OD=6∠PDC=∠AOP=∠POB=45°
不难证明:△PMO≌△PCD△PAM≌△PBC
∴PC=PM∠APM=∠BPC
又:∠MPN=45° 故:∠APM+∠BPN=45°
故:∠CPN=∠BPC+∠BPN=∠APM+∠BPN=45°=∠MPN
又:PN=PN PC=PM
∴△PMN≌△PCN
∴MN=CN
∴△MON的周长=OM+ON+MN=CD+ON+CN=OD=6.
故答案为:6.
本题主要考查了旋转的性质,正确作出辅助线构造全等的三角形是解题的关键.

解:作PA⊥y轴,PB⊥x轴.在x轴上截取BD=OA=OB=3,再截取DC=OM.
因为PA=PB=BD=OA=OB=3
故:OD=6∠PDC=∠AOP=∠POB=45°
不难证明:△PMO≌△PCD△PAM≌△PBC
∴PC=PM∠APM=∠BPC
又:∠MPN=45° 故:∠APM+∠BPN=45°
故:∠CPN=∠BPC+∠BPN=∠APM+∠BPN=45°=∠MPN
又:PN=PN PC=PM
∴△PMN≌△PCN
∴MN=CN
∴△MON的周长=OM+ON+MN=CD+ON+CN=OD=6.
故答案为:6.
本题主要考查了旋转的性质,正确作出辅助线构造全等的三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,1)关于x轴对称的点的坐标是
,1)关于x轴对称的点的坐标是 ) D (1.
) D (1. 中自变量x的取值范围是 .
中自变量x的取值范围是 . 中,自变量x的取值范围是
中,自变量x的取值范围是



 ,试研究该函数的性质.
,试研究该函数的性质. .
.
 的图象经过点A(1,-1),那么
的图象经过点A(1,-1),那么 ____,该函数图象与
____,该函数图象与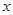 轴的交点坐标是_____,与
轴的交点坐标是_____,与 轴的交点坐标是_____
轴的交点坐标是_____
