题目内容
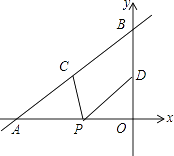
【题目】如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中有( )个是正确的。
①∠DAF=45° ②△ABE≌△ACD ③AD平分∠EDF ④![]()

A. 4B. 3C. 2D. 1
【答案】B
【解析】
①根据旋转的性质可得出∠BAE=∠CAF,由∠BAC=90°、∠DAE=45°可得出∠CAD+∠CAF=45°,即可判断①;②根据旋转的性质可得出△BAE≌△CAF,不能推出△BAE≌△CAD,即可判断②;③根据∠DAE=∠DAF=45°,根据角平分线定义即可判断③;④根据全等三角形的判定求出△AED≌△AFD,推出DE=DF,求出∠DCF=90°,根据勾股定理推出即可.
∵在Rt△ABC中,AB=AC,
∴∠B=∠ACB=45°,
①由旋转,可知:∠CAF=∠BAE,
∵∠BAD=90°,∠DAE=45°,
∴∠CAD+∠BAE=45°,
∴∠CAF+∠BAE=∠DAF=45°,故①正确;
②由旋转,可知:△ABE≌△ACF,不能推出△ABE≌△ACD,故②错误;
③∵∠EAD=∠DAF=45°,
∴AD平分∠EAF,故③正确;
④由旋转可知:AE=AF,∠ACF=∠B=45°,
∵∠ACB=45°,
∴∠DCF=90°,
由勾股定理得:CF2+CD2=DF2,
即BE2+DC2=DF2,
在△AED和△AFD中,
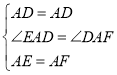 ,
,
∴△AED≌△AFD(SAS),
∴DE=DF,
∴BE2+DC2=DE2,故④正确.
故选B.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目