题目内容
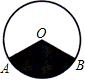 如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是
如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是
- A.1
- B.

- C.

- D.2
B
分析:利用扇形的半径以及以及在圆中所占比例,得出圆心角的度数,再利用圆锥底面圆周长等于扇形弧长求出即可.
解答:∵⊙O中,半径OA=4,∠AOB=120°,
∴扇形弧长为:l= =
=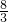 π,
π,
则由圆锥的底面圆的周长为:c=2πr=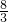 π.
π.
解得:r= .
.
故选B.
点评:此题主要主要考查了扇形组成圆锥后各部分对应情况,根据题意得出圆锥底面圆周长等于扇形弧长是解决问题的关键.
分析:利用扇形的半径以及以及在圆中所占比例,得出圆心角的度数,再利用圆锥底面圆周长等于扇形弧长求出即可.
解答:∵⊙O中,半径OA=4,∠AOB=120°,
∴扇形弧长为:l=
 =
=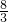 π,
π,则由圆锥的底面圆的周长为:c=2πr=
 π.
π.解得:r=
 .
.故选B.
点评:此题主要主要考查了扇形组成圆锥后各部分对应情况,根据题意得出圆锥底面圆周长等于扇形弧长是解决问题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
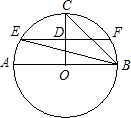 如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,则∠CBE=
如图,⊙O中,半径CO垂直于直径AB,D为OC的中点,过D作弦EF∥AB,则∠CBE= (2012•铁岭)如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是( )
(2012•铁岭)如图,⊙O中,半径OA=4,∠AOB=120°,用阴影部分的扇形围成的圆锥底面圆的半径长是( )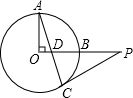 如图在⊙O中,半径OA⊥OB,C是⊙O上的一点,连接AC交OB于点D,P是OB延长线上一点,且满足PD=PC,求证:PC是⊙O的切线.
如图在⊙O中,半径OA⊥OB,C是⊙O上的一点,连接AC交OB于点D,P是OB延长线上一点,且满足PD=PC,求证:PC是⊙O的切线.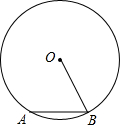 如图在⊙O中,半径OB=10,弦AB=10,则弦AB所对圆周角为
如图在⊙O中,半径OB=10,弦AB=10,则弦AB所对圆周角为