题目内容
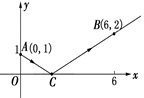
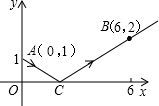 如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则光线从A点到B点经过的路线长度为
如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则光线从A点到B点经过的路线长度为
- A.6
- B.
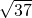
- C.3

- D.8
C
分析:根据入射角等于反射角得出∠ACO=∠BCD,根据∠AOC=∠BDC=90°,推出△AOC∽△BDC,得出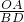 =
= ,代人求出OC、DC,根据勾股定理求出AC、BC,即可求出答案.
,代人求出OC、DC,根据勾股定理求出AC、BC,即可求出答案.
解答:
过B作BD⊥x轴于D,
∵A(0,1),B(6,2),
∴OA=1,OD=6,BD=2,
∵入射角等于反射角,
∴∠ACO=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△BDC,
∴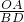 =
= ,
,
∴ =
=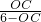 ,
,
解得:OC=2,DC=4,
在△AOC中,由勾股定理得:AC=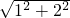 =
= ,
,
在△BDC中,由勾股定理得:BC=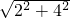 =2
=2 ,
,
∴AC+BC=3 ,
,
故选C.
点评:本题考查了勾股定理,坐标与图形性质,相似三角形的性质和判定,关键是求出AC和BC的长,主要考查学生运用性质进行推理和计算的能力.
分析:根据入射角等于反射角得出∠ACO=∠BCD,根据∠AOC=∠BDC=90°,推出△AOC∽△BDC,得出
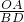 =
= ,代人求出OC、DC,根据勾股定理求出AC、BC,即可求出答案.
,代人求出OC、DC,根据勾股定理求出AC、BC,即可求出答案.解答:

过B作BD⊥x轴于D,
∵A(0,1),B(6,2),
∴OA=1,OD=6,BD=2,
∵入射角等于反射角,
∴∠ACO=∠BCD,
∵∠AOC=∠BDC=90°,
∴△AOC∽△BDC,
∴
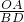 =
= ,
,∴
 =
=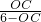 ,
,解得:OC=2,DC=4,
在△AOC中,由勾股定理得:AC=
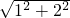 =
= ,
,在△BDC中,由勾股定理得:BC=
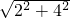 =2
=2 ,
,∴AC+BC=3
 ,
,故选C.
点评:本题考查了勾股定理,坐标与图形性质,相似三角形的性质和判定,关键是求出AC和BC的长,主要考查学生运用性质进行推理和计算的能力.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
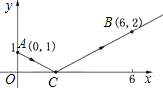 如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则光线从A点到B点经过的路线的长度为
如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则光线从A点到B点经过的路线的长度为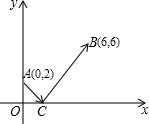 如图,一束光线从y轴的点A(0,2)出发,经过x轴上的点C反射后经过点B(6,6),则光线从点A到点B所经过的路程是( )
如图,一束光线从y轴的点A(0,2)出发,经过x轴上的点C反射后经过点B(6,6),则光线从点A到点B所经过的路程是( )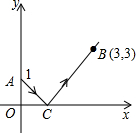 如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),则光线从A点到B点经过的路线长是
如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),则光线从A点到B点经过的路线长是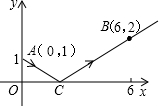 如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则光线从A点到B点经过的路线长度为( )
如图,一束光线从y轴上点A(0,1)发出,经过x轴上点C反射后,经过点B(6,2),则光线从A点到B点经过的路线长度为( )