题目内容
（2008•徐汇区一模）如图，在△ABC中，AH是BC边上的高，矩形DEFG内接于△ABC（即点D、E、F、G都在△ABC的边上），BC=18，AH=6，矩形DEFG的周长是20．求：S矩形DEFG的值．
分析：由四边形DEFG是矩形，可得△ADG∽△ABC，根据相似三角形对应高的比等于相似比，可得
=
，然后设DE=x，则由题意，得DG=10-x，即可得方程：
=
，解此方程即可求得答案．
| DG |
| BC |
| AM |
| AH |
| 10-x |
| 18 |
| 6-x |
| 6 |
解答：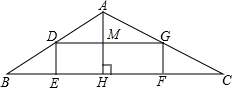
解：记AH与DG的交点为M．
∵四边形DEFG是矩形，
∴DG∥EF，
∴△ADG∽△ABC，
∵AH⊥BC，
∴AM⊥DG，
∴MH=DE，
∴
=
，
设DE=x，则由题意，得DG=10-x，
又∵BC=18，AH=6，
∴
=
，
解得x=4，
∴DE=4，DG=10-4=6，
∴S矩形DEFG=DE•DG=4×6=24．
解：记AH与DG的交点为M．∵四边形DEFG是矩形，
∴DG∥EF，
∴△ADG∽△ABC，
∵AH⊥BC，
∴AM⊥DG，
∴MH=DE，
∴
| DG |
| BC |
| AM |
| AH |
设DE=x，则由题意，得DG=10-x，
又∵BC=18，AH=6，
∴
| 10-x |
| 18 |
| 6-x |
| 6 |
解得x=4，
∴DE=4，DG=10-4=6，
∴S矩形DEFG=DE•DG=4×6=24．
点评：此题考查了相似三角形的判定与性质以及矩形的性质．此题难度适中，注意掌握数形结合思想与方程思想的应用．
练习册系列答案
相关题目
（2008•徐汇区一模）如图，直线l1∥l2∥l3，另两条直线分别交l1，l2，l3于点A，B，C及点D，E，F，且AB=3，DE=4，EF=2，则BC=
（2008•徐汇区一模）如图，DE∥BC，