题目内容
1)如图1,圆内接△ABC中,AB=BC=CA,OD、OE为⊙O的半径,OD⊥BC于点F,OE⊥AC于点G,求证:阴影部分四边形OFCG的面积是△ABC的面积的![]() .
.
(2)如图2,若∠DOE保持120°角度不变,求证:当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的![]() .
.

(1)证明:过点O作OH⊥AB于点H.
∵等边△ABC是⊙O的内接三角形,OD⊥BC ,OH⊥AB,OE⊥AC
∴∠B=∠C=60°,∠BHO=∠BFO=∠CFO=∠CGO=90°, BH=BF=CF=CG,OH=OF=OG
∴∠FOH=∠FOG=180°-60°=120°,∴四边形BDOH≌四边形CFOG
同理:四边形BDOH≌四边形AHOG
∴四边形BDOH≌四边形CFOG≌四边形AHOG
∴![]() ,
,
又∵![]()
∴![]() .
.
(2)证明:过圆心O分别作OM⊥BC,ON⊥AC,垂足为M、N.
则有∠OMF=∠ONG=90°,OM=ON,∠MON=∠FOG=120°
∴∠MON-∠FON=∠FOG-∠FON,即∠MOF=∠NOG
∴△MOF≌△NOG,∴![]()
∴若∠DOE保持120°角度不变,当∠DOE绕着O点旋转时,由两条半径和△ABC的两条边围成的图形(图中阴影部分)面积始终是△ABC的面积的![]() .
.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
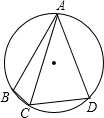 如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为( )
如图:在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边ABCD的面积为( )| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
 16、如图△ABC是圆内接三角形,AB是直径,BC=4cm,∠A=30°,则AB=
16、如图△ABC是圆内接三角形,AB是直径,BC=4cm,∠A=30°,则AB=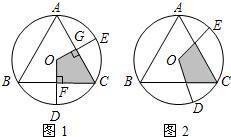 中阴影部分)面积始终是△ABC的面积的
中阴影部分)面积始终是△ABC的面积的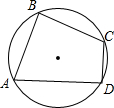 如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,则BC=
如图,在圆内接四边形ABCD中,∠A=60°,∠B=90°,AB=2,CD=1,则BC=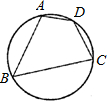 16、已知如图,在圆内接四边形ABCD中,∠B=30°,则∠D=
16、已知如图,在圆内接四边形ABCD中,∠B=30°,则∠D=