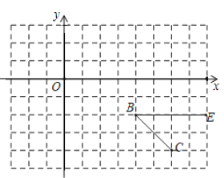
题目内容
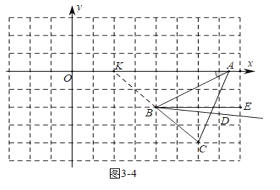
【题目】如图,平面直角坐标系中,![]()
![]() 轴,点
轴,点![]() 从原点
从原点![]() 出发在
出发在![]() 轴上以
轴上以![]() 单位/秒的速度向
单位/秒的速度向![]() 轴的正方向运动,运动的时间为
轴的正方向运动,运动的时间为![]() 秒.
秒.![]() 平分
平分![]() . (提示:
. (提示:![]() 中,
中,![]() ,若
,若![]() 则
则![]() ,反之亦然)
,反之亦然)
(1)当![]() 时,
时,![]() ;
;
(2)当![]() 的面积为
的面积为![]() 时,求
时,求![]() 点运动的时间
点运动的时间![]() ;
;
(3)当![]() 时,求
时,求![]() 的度数(用含
的度数(用含![]() 的式子表示,且不含绝对值).
的式子表示,且不含绝对值).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或
或![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
【解析】
(1)求出点A的坐标即可判断.
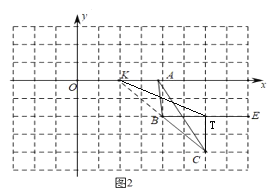
(2)如图2中,延长CB交x轴于K,则看(2,0).设A(n,0).根据S△ABC=S△AKCS△AKB=3,解方程求出n即可解决问题.
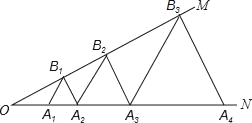
(3)分四种情形:如图31中,当0<t<2时,∠DBE=∠CBD+∠CBE.如图32中,当t=2时,∠DBE=45°或135°.如图33中,当2<t≤6时,∠DBE=∠ABE=∠ABD.如图34中,当t>6时,∠DBE=∠CBE∠CBD,分别求解即可解决问题.
(1)如图1中,
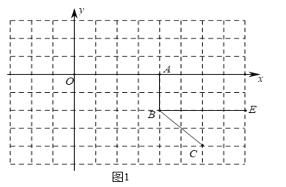
当t=4时,OA=4,
∴A(4,0),
∵B(4,2),
∴AB⊥OA,
∴∠OAB=90°,即m=90.
故答案为90.
![]() 延长
延长![]() 交
交![]() 轴于点
轴于点![]() ,
,
过![]() 作
作![]() 于点
于点![]()
连接![]()
![]()
![]()
设A(n,0).
又S△ABC=S△AKCS△AKB=3
![]()
解得n=5或n=-1(舍去)
![]() 时,
时,![]() 的面积为
的面积为![]() ;
;
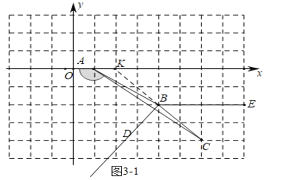
(3)如图31中,当0<t<2时,
∵∠ABC=(180°m°)+(180°45°)=315m°,BD平分∠ABC,
∴∠CBD=![]() ∠ABC=
∠ABC=![]()
∴∠DBE=∠CBD+∠CBE=![]() +45°=
+45°=![]()
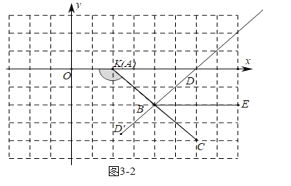
如图32中,当t=2时,∠DBE=45°或135°
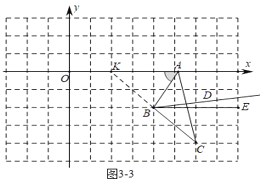
如图33中,当2<t≤6时,
∵OA∥BE,
∴∠ABE=∠OAB=m°,
∴∠ABC=45°+m°,
∵BD平分∠ABC,
∴∠ABD=![]() ,
,
∴∠DBE=∠ABE∠ABD=m°![]() =
=![]()
如图34中,当t>6时,同法可得:∠DBE=∠CBE∠CBD=45°![]() =
=![]() ;
;
综上,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 或
或![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.