题目内容
【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是
( )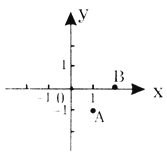
A.(3,-1)
B.(-1,-1)
C.(1,1)
D.(-2,-1)
【答案】D
【解析】
根据以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,根据平行四边形的判定分别对答案A,B,C,D进行分析即可得出符合要求的答案.
A、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,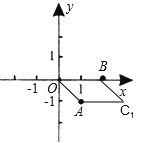
当第四个点为(3,-1)时,
∴BO=AC1=2,
∵A,C1 , 两点纵坐标相等,
∴BO∥AC1 ,
∴四边形OAC1B是平行四边形;故此选项正确;
B、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,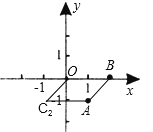
当第四个点为(-1,-1)时,
∴BO=AC2=2,
∵A,C2 , 两点纵坐标相等,
∴BO∥AC2 ,
∴四边形OC2AB是平行四边形;故此选项正确;
C、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,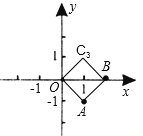
当第四个点为(1,1)时,
∴BO=AC1=2,
∵A,C1 , 两点纵坐标相等,
∴C3O=BC3=![]() ,
,
同理可得出AO=AB=![]() ,
,
进而得出C3O=BC3=AO=AB,∠OAB=90°,
∴四边形OABC3是正方形;故此选项正确;
D、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,
当第四个点为(-1,-1)时,四边形OC2AB是平行四边形;
∴当第四个点为(-2,-1)时,四边形OC2AB不可能是平行四边形;
故此选项错误.
故选D.
【考点精析】解答此题的关键在于理解平行四边形的性质的相关知识,掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】在小方格纸上按下面的方式涂色:

① ② ③ ④
(1)填表:
图形编号 | ① | ② | ③ | ④ | ⑤ | ⑥ |
涂色的小方格数 |
(2)像这样,第 n 个图形要涂色的小方格数是__________,第100个图形要涂色的小方格数是____________