题目内容
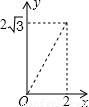
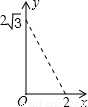
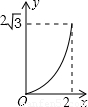
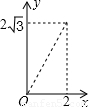
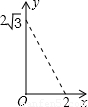
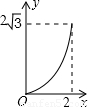
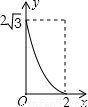
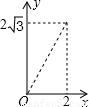
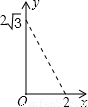
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线 ,与⊙O过A点的切线交于点B,且∠APB=60°,设OP= x,则△PAB的面积y关于x的函数图像大致是【 】
,与⊙O过A点的切线交于点B,且∠APB=60°,设OP= x,则△PAB的面积y关于x的函数图像大致是【 】

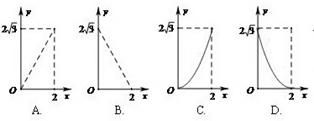
【答案】
D
【解析】动点问题的函数图象,锐角三角函数定义,特殊角的三角函数值。
利用AB与⊙O相切,△BAP是直角三角形,把直角三角形的直角边表示出来,从而用x表示出三角形的面积,根据函数解析式确定函数的图象:
∵AB与⊙O相切,∴∠BAP=90°,
∵OP=x,AP=2-x,∠BPA=60°,∴AB= ,
,
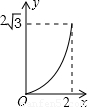
∴△APB的面积 ,(0≤x≤2)。
,(0≤x≤2)。
∴△PAB的面积y关于x的函数图像是经过(2,0)的抛物线在0≤x≤2的部分。故选D。

练习册系列答案
相关题目
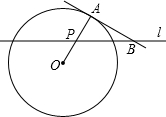 (2012•安徽)如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
(2012•安徽)如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )