题目内容
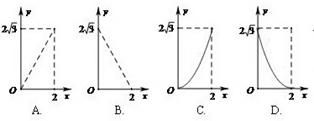
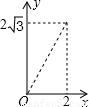
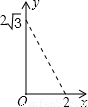
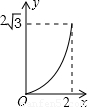
如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A.
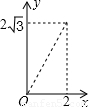
B.
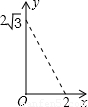
C.
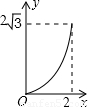
D.
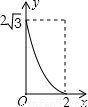
【答案】分析:根据已知得出S与x之间的函数关系式,进而得出函数是二次函数,当x=- =2时,S取到最小值为:
=2时,S取到最小值为: =0,即可得出图象.
=0,即可得出图象.
解答: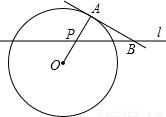 解:当P与O重合,
解:当P与O重合,
∵A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,
∴AO=2,OP=x,则AP=2-x,
∴tan60°=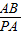 =
= ,
,
解得:AB= (2-x)=-
(2-x)=- x+2
x+2 ,
,
∴S△ABP= ×PA×AB=
×PA×AB= (2-x)•
(2-x)•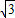 •(-x+2)=
•(-x+2)=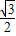 x2-2
x2-2 x+2
x+2 ,
,
故此函数为二次函数,
∵a= >0,
>0,
∴当x=- =2时,S取到最小值为:
=2时,S取到最小值为: =0,
=0,
根据图象得出只有D符合要求.
故选:D.
点评:此题主要考查了动点函数的图象,根据已知得出S与x之间的函数解析式是解题关键.
 =2时,S取到最小值为:
=2时,S取到最小值为: =0,即可得出图象.
=0,即可得出图象.解答:
 解:当P与O重合,
解:当P与O重合,∵A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,
∴AO=2,OP=x,则AP=2-x,
∴tan60°=
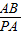 =
= ,
,解得:AB=
 (2-x)=-
(2-x)=- x+2
x+2 ,
,∴S△ABP=
 ×PA×AB=
×PA×AB= (2-x)•
(2-x)•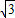 •(-x+2)=
•(-x+2)=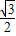 x2-2
x2-2 x+2
x+2 ,
,故此函数为二次函数,
∵a=
 >0,
>0,∴当x=-
 =2时,S取到最小值为:
=2时,S取到最小值为: =0,
=0,根据图象得出只有D符合要求.
故选:D.
点评:此题主要考查了动点函数的图象,根据已知得出S与x之间的函数解析式是解题关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
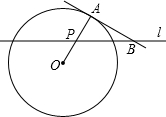 (2012•安徽)如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
(2012•安徽)如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
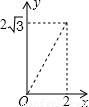
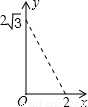
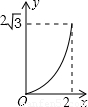



 ,与⊙O过A点的切线交于点B,且∠APB=60°,设OP= x,则△PAB的面积y关于x的函数图像大致是【 】
,与⊙O过A点的切线交于点B,且∠APB=60°,设OP= x,则△PAB的面积y关于x的函数图像大致是【 】