题目内容
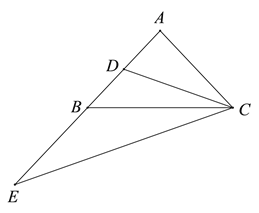
【题目】如图,在△ABC中,AB=AC,CD是AB边上的中线,延长AB至点E,使BE=AB,连接CE. 请你探究:
(1)当∠BAC为直角时,直接写出线段CE与CD之间的数量关系;
(2)当∠BAC为锐角或钝角时,(1)中的上述数量关系是否仍然成立?若成立,请给出证明;若不成立,请说明理由。
【答案】(1)CE=2CD;(2)仍然成立
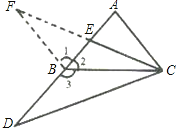
【解析】试题分析:(1)如图,延长CE到F,使EF=CE,连接FB.由CE是AB边上的中线,∠BEF=∠AEC,可证得△AEC≌△BEF,进而得∠1=∠A,FB=BD,从而可得△CDB≌△CFB,即可得到结果;
(2)根据上面的方法,直接可画图证明即可.
试题解析:(1)CE=2CD;
延长CE到F,使EF=CE,连接FB,
∵CE是AB边上的中线,
∴AE=BE,
又∵∠BEF=∠AEC,
∴△AEC≌△BEF,
∴FB=AC,∠1=∠A,
∵BD=AB,
∴FB=BD,
∵∠3=∠A+∠ACB=∠1+∠2,即∠CBD=∠CBF,
又∵BC为公共边,
∴△CDB≌△CFB,
∴CD=CF=2CE,
即2CE=CD
(2)仍然成立. 例如取AC中点M,连接BM. 证法较多,略。

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案
相关题目




