题目内容
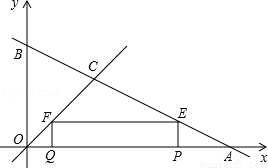
如图,直线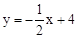 与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).
(1)求点P运动的速度是多少?
(2)当t为多少秒时,矩形PEFQ为正方形?
(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.
解:(1)∵直线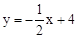 与坐标轴分别交于点A、B,
与坐标轴分别交于点A、B,
∴x=0时,y=4;y=0时,x=8。∴BO=4,AO=8。∴ 。
。
当t秒时,QO=FQ=t,则EP=t,
∵EP∥BO,∴△ABO∽△ARP。∴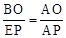 ,即
,即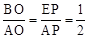 。
。
∴AP=2t。
∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,
∴点P运动的速度是每秒2个单位长度。
(2)∵当OP=OQ时,PE与QF重合,此时t= ,当点P、Q其中一点停止运动时,另一点也停止运动,
,当点P、Q其中一点停止运动时,另一点也停止运动,
∴分0<t< 和
和 <t≤4两种情况讨论:
<t≤4两种情况讨论:
如图1,当0<t< 。即点P在点Q右侧时,若PQ=PE,矩形PEFQ为正方形,
。即点P在点Q右侧时,若PQ=PE,矩形PEFQ为正方形,
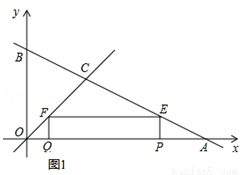
∵OQ=FQ=t,PA=2t,
∴QP=8-t-2t=8-3t。
∴8-3t=t。
解得:t=2。
如图2,当 <t≤4,即点P在点Q左侧时,若PQ=PE,矩形PEFQ为正方形,∵OQ=t,PA=2t,∴OP=8-2t。
<t≤4,即点P在点Q左侧时,若PQ=PE,矩形PEFQ为正方形,∵OQ=t,PA=2t,∴OP=8-2t。

∴ 。
。
∴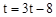 。
。
解得:t=4。
∴当t为2秒或4秒时,矩形PEFQ为正方形。
(3)同(2)分0<t< 和
和 <t≤4两种情况讨论:
<t≤4两种情况讨论:
如图1,当0<t< 时,Q在P点的左边
时,Q在P点的左边
∵OQ=t,PA=2t,∴QP=8-t-2t=8-3t,
∴ 。
。
∴当t= 时,S的最大值为
时,S的最大值为 ,
,
如图2,当 <t≤4时,Q在P点的右边,
<t≤4时,Q在P点的右边,
∵OQ=t,PA=2t,∴ 。
。
∴ 。
。
∵当 <t≤4时,S随t的增大而增大,∴t=4时,S的最大值为:3×42﹣8×4=16。
<t≤4时,S随t的增大而增大,∴t=4时,S的最大值为:3×42﹣8×4=16。
综上所述,当t=4时,S的最大值为:16。
【解析】
试题分析:(1)根据直线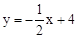 与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出
与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,得出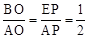 ,据此可以求得点P的运动速度。
,据此可以求得点P的运动速度。
(2)当PQ=PE时,以及当PQ=PE时,矩形PEFQ为正方形,分别求出即可。
(3)根据(2)中所求得出S与t的函数关系式,从而利用二次函数性质求出即可。

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案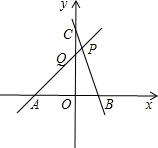 出点D的坐标;若不存在,请说明理由.
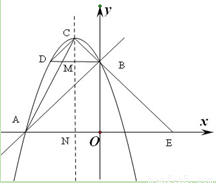
出点D的坐标;若不存在,请说明理由.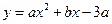 经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。
经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。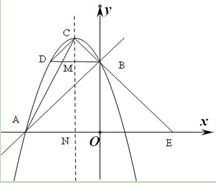
 的图象,直线PB是一次函数
的图象,直线PB是一次函数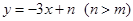 的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点。
的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点。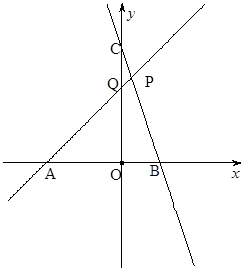
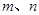 分别表示点A、B、P的坐标及∠PAB的度数;
分别表示点A、B、P的坐标及∠PAB的度数;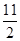 ,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;
,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;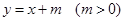 的图象,直线PB是一次函数
的图象,直线PB是一次函数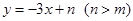 的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点。
的图象,点P是两直线的交点,点A、B、C、Q分别是两条直线与坐标轴的交点。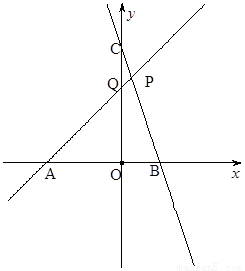
 分别表示点A、B、P的坐标及∠PAB的度数;
分别表示点A、B、P的坐标及∠PAB的度数; ,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式;
,且CQ:AO=1:2,试求点P的坐标,并求出直线PA与PB的函数表达式; 经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。
经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。