Question

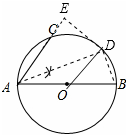
如图，AB是⊙O的直径，AC是弦．

（1）请你按下面步骤画图（画图或作辅助线时先使用铅笔画出，确定后必须使用黑色字迹的签字笔描黑）；
第一步，过点A作∠BAC的角平分线，交⊙O于点D；
第二步，过点D作AC的垂线，交AC的延长线于点E．
第三步，连接BD．
（2）求证：DE是⊙O的切线；
（3）如图AD=5，AE=4，求⊙O的直径．

Answer 1

（1）如下图；（2）详见解析；（3）

试题分析：（1）根据基本作图作出∠BAC的角平分线AD交⊙O于点D；点D作AC的垂线，垂足为点E；
（2）连接OD，先根据圆的基本性质可得OA=OD，根据“等边对等角”可得∠OAD=∠ODA，再结合AD平分∠BAC可得∠EAD=∠ODA，即可证得AC∥OD，然后根据平行线的性质即可作出判断；
（3）根据直径所对的圆周角为直角得到∠ADB=90°，而DE⊥AC，则∠AED=90°，又由AD平分∠CAB得到△AED∽△ADB，再根据相似三角形的对应边成比例即可求得结果.
试题解析：（1）如图所示：

（2）连接OD

∵OA=OD
∴∠OAD=∠ODA，
∵AD平分∠BAC
∴∠EAD=∠OAD
∴∠EAD=∠ODA
∴AC∥OD
∵DE⊥AC
∴∠EDO=90°
∴DE是⊙O的切线；
（3）∵AB是⊙O的直径，
∴∠ADB=90°，
∵DE⊥AC，
∴∠AED=90°，
∵AD平分∠CAB，
∴∠CAD=∠DAB，
∴Rt△ADE∽Rt△ABD，
∴
∵AD=5，AE=4
∴，解得，即⊙O的直径为．