题目内容
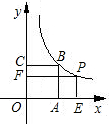如图：在函数y=| 4 |
| x |
| A、矩形BCFG和矩形GAEP面积相等 |
| B、矩形FOEP和正方形COAB面积相等 |
| C、点B的坐标是（4，4） |
| D、图象关于过O、B两点的直线对称 |
分析：由于B、P在函数y=
（x＞0）的图象上，由k的几何意义判断各个说法．
| 4 |
| x |
解答：解：A、矩形BCFG和矩形GAEP面积相等，正确，都等于4-S矩形AGFO；
B、矩形FOEP和正方形COAB面积相等，正确，都等于4；
C、点B的坐标是（4，4），错误，应为（2，2）；
D、图象关于过O、B两点的直线（即y=x）对称．
故选C．
B、矩形FOEP和正方形COAB面积相等，正确，都等于4；
C、点B的坐标是（4，4），错误，应为（2，2）；
D、图象关于过O、B两点的直线（即y=x）对称．
故选C．
点评：本题主要考查了反比例函数y=
中k的几何意义，即过双曲线上任意一点引x轴、y轴垂线，所得矩形面积为|k|，是经常考查的一个知识点．
| k |
| x |
练习册系列答案
相关题目
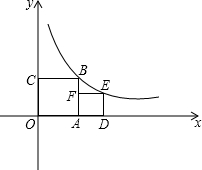如图，正方形OABC，ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B，E在函数y=| 4 |
| x |
A、（
| ||||
B、（3+
| ||||
C、（
| ||||
D、（3-
|
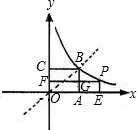如图，在函数y=| 4 |
| x |
| A、长方形BCFG和长方形GAEP的面积相等 |
| B、点B的坐标是（4，4） |
| C、图象关于过OB的直线对称 |
| D、矩形FOEP与正方形COAB的面积相等 |
（2013•连云港模拟）如图，在函数
如图，在函数