题目内容
直线y=-x+7与y轴、x轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,顶点为C,直线AB与抛物线的对称轴交于点D.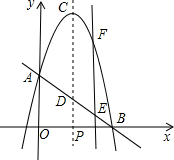
(1)求A、B坐标,并求抛物线的表达式;
(2)若点P以每秒1个单位长度的速度从点B沿x轴向点O运动,过P作PF∥CD交直线AB于点E,交抛物线于点F,设点P的运动时间为t秒.
①用含t的代数式表示线段EF的长;当t取何值时线段EF有最大值,求出这个最大值;
②是否存在这样的t值,使得四边形EFCD是平行四边形?若存在则求出t的值;若不存在,请说明理由.
分析:(1)利用直线的解析式可以求出A、B的坐标,利用A、B的坐标根据待定系数法就可以求出抛物线的解析式.
(2)①先表示出P点的坐标,利用P点的横坐标就可以求出E点F点的坐标,利用E、F的总坐标就可以表示出EF的长度.然后化为顶点式就可以求出其最大值.
②利用对称轴与AB的交点就可以求出D点的坐标,利用C、D的坐标就可以求出CD的长度,再代入EF的解析式就可以求出其t的值.
(2)①先表示出P点的坐标,利用P点的横坐标就可以求出E点F点的坐标,利用E、F的总坐标就可以表示出EF的长度.然后化为顶点式就可以求出其最大值.
②利用对称轴与AB的交点就可以求出D点的坐标,利用C、D的坐标就可以求出CD的长度,再代入EF的解析式就可以求出其t的值.
解答:解:(1)令x=0,则y=7,
∴A(0,7).
令y=0,则x=7,
∴B(7,0).
把(0,7),(7,0)代入抛物线的解析式为:
,
解得
.
∴抛物线的解析式为:y=-x2+6x+7;
(2)①设P(7-t,0).
∴F(7-t,-t2+8t),E(7-t,t),
∴EF=-t2+8t-t,
即EF=-t2+7t(0≤t≤7),
∵EF=-(t-
)2+
,
∴当t=
时,EF有最大值
;
②抛物线y=-x2+6x+7的解析式变形为:
y=-(x-3)2+16,
∴顶点C(3,16).
当x=3时,y=-3+7,y=4,
∴D(3,4),
∴CD=12,
∴P点在对称轴的右侧.
∵四边形EFCD是平行四边形,
∴CD=EF=12
∴-t2+7t=12,
解得t=3或t=4(舍去)
∴满足条件t的值为3.
∴A(0,7).
令y=0,则x=7,
∴B(7,0).
把(0,7),(7,0)代入抛物线的解析式为:
|
解得
|
∴抛物线的解析式为:y=-x2+6x+7;
(2)①设P(7-t,0).
∴F(7-t,-t2+8t),E(7-t,t),
∴EF=-t2+8t-t,
即EF=-t2+7t(0≤t≤7),
∵EF=-(t-
| 7 |
| 2 |
| 49 |
| 4 |
∴当t=
| 7 |
| 2 |
| 49 |
| 4 |
②抛物线y=-x2+6x+7的解析式变形为:
y=-(x-3)2+16,
∴顶点C(3,16).
当x=3时,y=-3+7,y=4,
∴D(3,4),
∴CD=12,
∴P点在对称轴的右侧.
∵四边形EFCD是平行四边形,
∴CD=EF=12
∴-t2+7t=12,
解得t=3或t=4(舍去)
∴满足条件t的值为3.
点评:本题考查了根据函数的解析式求交点坐标,根据点的坐标求函数的解析式,平行四边形的判定及性质等多个知识点.

练习册系列答案
相关题目
 内作Rt△ABC,∠BAC=90°.
内作Rt△ABC,∠BAC=90°.
 过B、C分别作y轴的平行线交双曲线
过B、C分别作y轴的平行线交双曲线 (2012•鄂州)直线y=-
(2012•鄂州)直线y=- (2013•威海)如图,在平面直角坐标系中,直线y=
(2013•威海)如图,在平面直角坐标系中,直线y=