题目内容

(2012•鄂州)直线y=-
x-1与反比例函数
y=(x<0)的图象交于点A,与x轴相交于点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为( )
分析:过A作AD⊥BC于D,先求出直线=-
x-1与x轴交点B的坐标(-2,0),则得到C点的横坐标为-2,由于C点在反比例函数y=
的图象上,可表示出C点坐标为(-2,-
),利用等腰三角形的性质,由AC=AB,AD⊥BC,得到DC=DB,于是D点坐标为(-2,-
),则可得到A点的纵坐标为-
,利用点A在函数y=
的图象上,可表示出点A的坐标为(-4,-
),然后把A(-4,-
)代入y=-
x-1得到关于k的方程,解方程即可求出k的值.
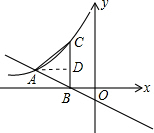
解答:解:过A作AD⊥BC于D,如图,
对于y=-
x-1,令y=0,则-
x-1=0,解得x=-2,
∴B点坐标为(-2,0),
∵CB⊥x轴,
∴C点的横坐标为-2,
对于y=
,令x=-2,则y=-
,
∴C点坐标为(-2,-
),
∵AC=AB,AD⊥BC,
∴DC=DB,
∴D点坐标为(-2,-
),
∴A点的纵坐标为-
,
而点A在函数y=
的图象上,
把y=-
代入y=
得x=-4,
∴点A的坐标为(-4,-
),
把A(-4,-
)代入y=-
x-1得-
=-
×(-4)-1,
∴k=-4.
故选B.
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数的交点坐标满足两个函数的解析式.也考查了与x轴垂直的直线上所有点的横坐标相同以及等腰三角形的性质.
 一题一题找答案解析太慢了
一题一题找答案解析太慢了
下载作业精灵直接查看整书答案解析立即下载
练习册系列答案
相关题目
 (2012•鄂州)直线y=-
(2012•鄂州)直线y=-


 新思维寒假作业系列答案
新思维寒假作业系列答案
 (2012•鄂州)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,试求BD的长.
(2012•鄂州)小明是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A、B、D在同一直线上,EF∥AD,∠A=∠EDF=90°,∠C=45°,∠E=60°,量得DE=8,试求BD的长. (2012•鄂州)如图OA=OB=OC且∠ACB=30°,则∠AOB的大小是( )
(2012•鄂州)如图OA=OB=OC且∠ACB=30°,则∠AOB的大小是( )