题目内容
已知△ABC与△A′B′C′的相似比为 ,△ABC与△A″B″C″的相似比为
,△ABC与△A″B″C″的相似比为 ,则△A′B′C′与△A″B″C″的相似比为
,则△A′B′C′与△A″B″C″的相似比为
- A.

- B.

- C.
 或
或
- D.
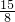
D
分析:由题意;已知△ABC与△A′B′C′的相似比为 ,△ABC与△A″B″C″的相似比为
,△ABC与△A″B″C″的相似比为 ,再根据相似三角形的传递性从而求出△A′B′C′与△A″B″C″的相似比.
,再根据相似三角形的传递性从而求出△A′B′C′与△A″B″C″的相似比.
解答:∵△ABC与△A′B′C′的相似比为 ,
,
∴ ,
,
∵△ABC与△A″B″C″的相似比为 ,
,
∴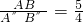 ,
,
∴△A′B′C′与△A″B″C″的相似比为:
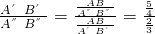 =
=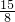 ,
,
故选D.
点评:此题考查了相似三角形的基本性质及对应边成比例,还考查了相似三角形的传递性.
分析:由题意;已知△ABC与△A′B′C′的相似比为
 ,△ABC与△A″B″C″的相似比为
,△ABC与△A″B″C″的相似比为 ,再根据相似三角形的传递性从而求出△A′B′C′与△A″B″C″的相似比.
,再根据相似三角形的传递性从而求出△A′B′C′与△A″B″C″的相似比.解答:∵△ABC与△A′B′C′的相似比为
 ,
,∴
 ,
,∵△ABC与△A″B″C″的相似比为
 ,
,∴
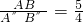 ,
,∴△A′B′C′与△A″B″C″的相似比为:
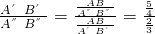 =
=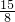 ,
,故选D.
点评:此题考查了相似三角形的基本性质及对应边成比例,还考查了相似三角形的传递性.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
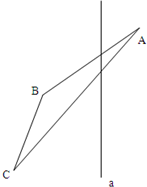 21、如图,已知△ABC与直线a、作出△ABC关于a的对称三角形△A′B′C′.(不写作法,保留作图痕迹)
21、如图,已知△ABC与直线a、作出△ABC关于a的对称三角形△A′B′C′.(不写作法,保留作图痕迹) 如图,在平面直角坐标系中,已知△ABC与△DEF关于点P中心对称
如图,在平面直角坐标系中,已知△ABC与△DEF关于点P中心对称