题目内容
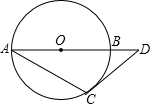 已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,则BD的长为
已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,则BD的长为
- A.2R
- B.
 R
R - C.R
- D.
 R
R
C
分析:先利用“同弧所对的圆周角是圆心角的一半”得出∠COD=2∠A=60°再解直角三角形可得CD长,最后用切割线定理可得BD长.
解答: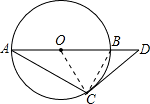 解:连接OC,BC,
解:连接OC,BC,
∵AB是圆O的直径,DC是圆O的切线,C是切点,
∴∠ACB=∠OCD=90°,
∵∠CAB=30°,
∴∠COD=2∠A=60°,CD=OC•tan∠COD= R,
R,
由切割线定理得,CD2=BD•AD=BD(BD+AB),
∴BD=R.
故选C.
点评:本题利用了直径对的圆周角是直角,切线的性质,切割线定理求解.
分析:先利用“同弧所对的圆周角是圆心角的一半”得出∠COD=2∠A=60°再解直角三角形可得CD长,最后用切割线定理可得BD长.
解答:
 解:连接OC,BC,
解:连接OC,BC,∵AB是圆O的直径,DC是圆O的切线,C是切点,
∴∠ACB=∠OCD=90°,
∵∠CAB=30°,
∴∠COD=2∠A=60°,CD=OC•tan∠COD=
 R,
R,由切割线定理得,CD2=BD•AD=BD(BD+AB),
∴BD=R.
故选C.
点评:本题利用了直径对的圆周角是直角,切线的性质,切割线定理求解.

练习册系列答案
相关题目
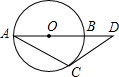 已知圆O的半径为5,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,则BD的长为
已知圆O的半径为5,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连接AC,若∠CAB=30°,则BD的长为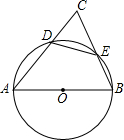 如图,在△ABC中,∠C=60°,以分别交AC,BC于点D,E,已知圆O的半径为
如图,在△ABC中,∠C=60°,以分别交AC,BC于点D,E,已知圆O的半径为