题目内容
【题目】如图,四边形ABCD是正方形,直线a,b,c分别通过A、D、C三点,且a∥b∥c.若a与b之间的距离是5,b与c之间的距离是7,则正方形ABCD的面积是( ) 
A.70
B.74
C.144
D.148
【答案】B
【解析】解:如图:
过A作AM⊥直线b于M,过D作DN⊥直线c于N,
则∠AMD=∠DNC=90°,
∵直线b∥直线c,DN⊥直线c,
∴∠2+∠3=90°,
∵四边形ABCD是正方形,
∴AD=DC,∠1+∠2=90°,
∴∠1=∠3,
在△AMD和△CND中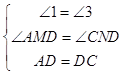
∴△AMD≌△CND,
∴AM=CN,
∵a与b之间的距离是5,b与c之间的距离是7,
∴AM=CN=5,DN=7,
在Rt△DNC中,由勾股定理得:DC2=DN2+CN2=72+52=74,
即正方形ABCD的面积为74,
故选B.
过A作AM⊥直线b于M,过D作DN⊥直线c于N,求出∠AMD=∠DNC=90°,AD=DC,∠1=∠3,根据AAS推出△AMD≌△CND,根据全等得出AM=CN,求出AM=CN=5,DN=7,在Rt△DNC中,由勾股定理求出DC2即可.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
【题目】某仓库原有某种货物库存270千克,现规定运入为正,运出为负,一天中七次出入如表(单位:千克)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
﹣30 | +82 | ﹣19 | +102 | ﹣96 | +34 | ﹣28 |
(1)在第次纪录时库存最多.
(2)求最终这一天库存增加或减少了多少?
(3)若货物装卸费用为每千克0.3元,问这一天需装卸费用多少元?

