题目内容
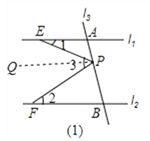
【题目】如图,已知直线l1∥l2,l3、l4和l1、l2分别交于点A、B、C、D,点P在直线l3或l4上且不与点A、B、C、D重合.记∠AEP=∠1,∠PFB=∠2,∠EPF=∠3.



(1)若点P在图(1)位置时,求证:∠3=∠1+∠2;
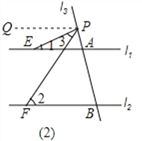
(2)著点P在图(2)位置时,请写出∠1、∠2、∠3之间的关系,并说明理由;
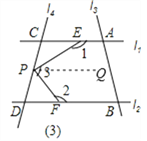
(3)若点P在图(3)位置时,写出∠1、∠2、∠3之间的关系
【答案】(1)证明见解析;(2)∠2=∠3+∠1, 理由见解析;(3)∠1+∠2+∠3=360°
【解析】分析:此题三个小题的解题思路是一致的,过P作直线![]() 、
、![]() 的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.
的平行线,利用平行线的性质得到和∠1、∠2相等的角,然后结合这些等角和∠3的位置关系,来得出∠1、∠2、∠3的数量关系.
本题解析:
(1)证明:过点P作PM∥l1 ∵l1∥l2, PM∥l1 ∴PM∥l2
∴∠2=∠FPM ∵PM∥l1 ∴∠1=∠EPM
∴∠3=∠FPM+∠EPM=∠2+∠1
(2)解:∠2=∠3+∠1 理由如下
过点P作PN∥l1 ∵l1∥l2, PN∥l1 ∴PN∥l2
∴∠2=∠FPM ∵PM∥l1 ∴∠1=∠EPM
∴∠2=∠FPM=∠3+∠EPM=∠3+∠1
(3)∠1+∠2+∠3=360°

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目