题目内容
(2012•河口区二模)(1)解方程:
+
=1
(2)当m为何值时,关于x的方程(m-2)x2-(2m-1)x+m=0有两个实数根.
| 2 |
| 2x-1 |
| 5 |
| 1-2x |
(2)当m为何值时,关于x的方程(m-2)x2-(2m-1)x+m=0有两个实数根.
分析:(1)先把分式方程去分母后变成整式方程,求出整式方程的解,再代入2x-1进行检验即可;
(2)根据方程有两个实数解得出[-(2m-1)]2-4(m-2)m≥0,且m-2≠0,求出即可.
(2)根据方程有两个实数解得出[-(2m-1)]2-4(m-2)m≥0,且m-2≠0,求出即可.
解答:(1)解:方程两边都乘以2x-1得:2-5=2x-1,
解这个方程得:2x=-2,
x=-1,
检验:∵把x=-1代入2x-1≠0,
∴x=-1是原方程的解;
(2)解:要使方程有两个实数根,必须[-(2m-1)]2-4(m-2)m≥0,且m-2≠0,
解得:m≥-
且m≠2,
答:当m≥-
且m≠2,时,关于x的方程(m-2)x2-(2m-1)x+m=0有两个实数根.
解这个方程得:2x=-2,
x=-1,
检验:∵把x=-1代入2x-1≠0,
∴x=-1是原方程的解;
(2)解:要使方程有两个实数根,必须[-(2m-1)]2-4(m-2)m≥0,且m-2≠0,
解得:m≥-
| 1 |
| 4 |
答:当m≥-
| 1 |
| 4 |
点评:本题考查了解分式方程和根的判别式,注意:解分式方程一定要进行检验,方程有两个解得条件是b2-4ac≥0且a≠0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

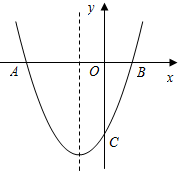 (2012•河口区二模)已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0)、C(0,-2).
(2012•河口区二模)已知:抛物线y=ax2+bx+c(a≠0)的对称轴为x=-1,与x轴交于A,B两点,与y轴交于点C,其中A(-3,0)、C(0,-2).