Question

（2013•西陵区模拟）在平行四边形ABCD中，AB=5，AD=3，sinA=

2

3

，点P是AB上一动点，（点P不与点A、点B重合），过点P作PQ∥AD交BD于Q，连结CQ，设AP的长为x，四边形QPBC的面积为y．
（1）计算平行四边形ABCD的面积；
（2）写出y关于x的函数解析式，并指出自变量x的取值范围；
（3）是否存在实数x，使得S_△BPQ=S_△BCQ？如果存在，求出x的值；如果不存在，请说明理由．

Answer 1

分析：（1）作DH⊥AB垂足为H，过Q作KR⊥AB交DC于K，交AB于R，求出DH，根据面积公式求出即可；
（2）求出QR，QK的值，分别求出△BPQ、△BDC、△DQC的面积，即可求出答案；
（3）根据（2）得出方程当

1

2

•（5-x）•

2(5-x)

5

=

1

2

×10-

1

2

×5×

2x

5

，求出即可．

解答：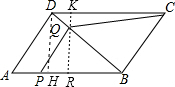
解：（1）作DH⊥AB垂足为H，过Q作KR⊥AB交DC于K，交AB于R，
∵sinA=

DH

AD

=

2

3

，
∴在Rt△ADH中，DH=AD•sinA=2，
∴S _□ABCD=AB•DH=5•2=10；

（2）∵PQ∥AD，
∴△BQP∽△BDA，
∴

PQ

AD

=

BP

AB

，

BP

AB

=

QR

DH

∴

PQ

3

=

5-x

5

，

5-x

5

=

QR

2

∴PQ=

3(5-x)

5

，QR=

2(5-x)

5

，
∴QK=2-

2(5-x)

5

=

2x

5

，
∴y=S_△BPQ+S_△BDC-S_△DQC=

1

2

•（5-x）•

2(5-x)

5

+

1

2

×10-

1

2

×5×

2x

5

，
y=

1

5

x²-3x+10（0＜x＜5）；

（3）不存在实数x，使得S_△BPQ=S_△BCQ，
理由是：假设存在x，使S_△BPQ=S_△BQC，
则

1

2

•（5-x）•

2(5-x)

5

=

1

2

×10-

1

2

×5×

2x

5

                                
解得  x₁=0或x₂=5                         
∵0＜x＜5，
∴不存在实数x，使S_△BPQ=S_△BCQ．

点评：本题考查了相似三角形的性质和判定，平行四边形的性质，三角形的面积的应用，主要考查学生的计算能力，注意：相似三角形的对应高之比等于对应边之比．